Conservation of angular momentum

1. Conservation of angular momentum

Like conservation of linear momentum, the principle of conservation angular momenum is a universal law, that follows from the equation Σ τ_ext = dL/dt; where:

It means when a net external torque acting on a system is zero, the total angular momentum of the system is constant (conserved). Un ice skater pirouetting takes the advantage of this principle.

2. Example

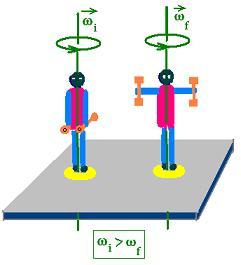
Another example is a person standing at the center of a turntable with two dumbbells of mass m each in each hand. The axial of the system is vertical and passes in the middle of the person through her/his center of mass. When the two hands are extended horizontally, the moment of inertia of the system is
I_i = I_{pers_ext} + I_{dumb_ext}. When the two arms are pulled, we have:
I_f = I_{pers_pul} + I_{dumb_pul}.

Where:
I_i is the initial moment of inertia of the system,
I_{pers_ext} is the moment of inertia of the person alone with arms extended,
I_{pers_pul} is the moment of inertia of the person alone with arms pulled to in to stomach,
I_{dumb_ext} is the moment of inertia of the two dumbells with arms extended = 2 m d_ext²,
I_{dumb_pul} is the moment of inertia of the two dumbells with arms pulled to in to stomach= 2 m d_pul², and
I_f is the final moment of inertia of the system.

The only external force acting on the system is the weight, which ha no torque with respect to the choice of the axial. The total angular momentum L, at any time, is constant. It is equal to I_cmω, where ω is angular velocity of the system about the axial.

The cnservation of angular momentum law is written as:
Constant = I_cmω = I_iω_i = I_fω_f

Therefore:

ω_f = I_iω_i/I_f =
(I_{pers_pul} + _{dumb_pul})ω_i/(I_{pers_ext} + I_{dumb_ext}) =
(I_{pers_pul} + 2 m d_pul²)ω_i/(I_{pers_ext} + 2 m d_ext²)

m = 5 Kg, d_pul = 0.2 m, d_ext = 1 m
I_{pers_pul} = 2.0 kg m², I_{pers_ext} = 3.0 kg.m²
ω_i = 1.3 revolutions per 1 second.

I_i = 2.0 + 2 x 5 x (0.2)² = 2.4 kg.m²
I_f = 3.0 + 2 x 5 x (1.0)² = 13.0 kg.m²

ω_f = I_iω_i/I_f = 2.4 x 1.3 /13.0 = 0.24 revolutions per second.
The angular speed decreases.


The corresponding kinetic energy is:
KE_i = (1/2) I_iω_i²
KE_f = (1/2) I_fω_f²

Therefore:
KE_i/KE_f = I_iω_i²/I_fω_f² = ω_i/ω_f = 1.3 /0.24 = 5.42
or
KE_f/KE_i = 1/5.24 = 0.185 = 18.5%

When the two arms become extended the system losses speed, then kinetic enery. When the arms are pulled, the system gain kinetic enery. This exchange of kinetic energy is due to the internal energy produced within the system. This internal energy is negative by extanding the arms, and positive when the arms are pulled.
Recall that the enery of a system is the sum of the energy of its center of mass plus the internal energy; which is the same measured in the reference frame of the center of mass or in the refrence frame of lab (at rest).