Angular momentum

1. Angular momentum

A force exerted on an object, that can be translated, causes its linear velocity to change: F = m a. A torque exerted on an object, that can be rotated, causes its angular velocity to change τ = I α. Any object can rotate about an axis. Let's recall that a moment(of force) is the tendency of the force to oscillate or rotate an object; and the momentumis the quantity of motion of an object. Linear momentum if the motion of the object is linear and uniform; and angular momentum when the motion of the object is circular. The linear momentum is a vector quantity as the velocity v is; and the angular momentum is also a vector as ω is. A linear momentum "P" has the same direction as the linear velocity v . The direction of the angular momentum "L" is the direction if the angular velocity "ω". The direction of ω is on the rotation axis. This direction is perpendicular to the plane from where the angular momentum stems; that is the plane formed by the position vector and the linear velocity (then linear momentum) of the object. We remember that the moment of inertia of an object is relative to an axis; whereas the torque and the angular momentum are relative to a reference point. The concept of angular momentum is very useful in rotational dynamics.

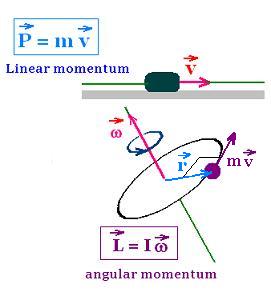
2. Angular momentum of a single particle

The angular momentum "l" of a particle about a referenec point O is defined as:

l = r x p

where r is the position vectore of the particle measured from O; and p is its linear momentum. The cross product shows that the linear momentum is a vector quantity. It is perpendicular to the plane containing r and p. Its direction is defined by the right-hand rule. Its dimension is [mass][length²][time ^-1]; and its SI unit is kg.m/s. Its magnitude is = mrvsinθ, where θ is the angle formed by r and p in this order. Recall:
The angular momentum is relative to reference point about which is defined and then calculated.

The simple case is when a particle travels in a circle of radius r. The angular momentum is the determined about the center of cercle, that is here, the point of reference. In circular motion, at each point of the circle, the velocity v is perpendicular to r, therefore θ = 90^o and the expression of the angular mmentum takes the following simple form:

l = r x p = r x mv = m r x v = m r v sin θ = mrv

Since v = ω r, we have then:
l = mr r ω = mωr²
If the vectors r and p are contained in the plane xy, l will point in the z-axis. Its direction depends on the sense of the rotation. It is given by the right-hand rule. Viewed from the + z direction, if the motion is counterclockwise, l is toward + z, hence l_z is positive. If the motion is clockwise, l is toward -z, and l_z is negative. This is exacly the direction of ω_z. If k is the unit vector of the z-axis, we can write:

If the motion is also uniform, ω_z will be constant equal to ω arewe will have:
l = l_z k = mωr² k

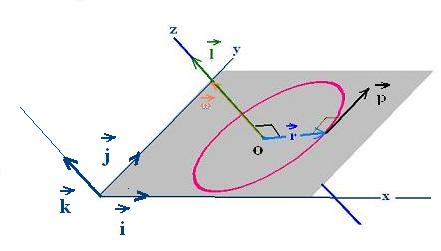
In an inertial frame, the second Newton's law is writen as ΣF = ma, where ΣF is the net force exerted on the particle of mass m, and a the produced acceleration. In terms of linear momentum, this equation is written as: ΣF = dp/dt; that is the derivative of the linear momentum p of the particle. In rotational motion, the net force ΣF exerted on a particle produces a torque a net torque Στ = r x ΣF, where r is the position vector of the particle nad ΣF is the net force exerted on the particle. We want to link this τ to angular momentum l of the particle.

With l = r x p. The time derivative of the angular momentum is: dl/dt = dr/dt x p + r x dp/dt
The first term der/dt x p =0 because dr/dt = v, and v x p = m v x v = 0. Therefore:
dl/dt = r x dp/dt = r x ΣF = Στ
We obtain, therefore an important formula:

2. Angular momentum of a system of particles

For a system of particles, the total angular momentum L relative to a reference point is equal to the vector sum of individual angular momenta l_i all relative to that same point, that is L = Σl_i. The time derivative of L is: dL/dt = Σdl_i/dt = Σ(Στ_i) (sum for all particles, and the sum of all torques for each particle, that is the sum for all particles of their net torques). This sum of net torques is equal to:
- The sum of the internal torques on the particles due the forces they exert on each other within the system, which they cancel in pairs (according to the Newton's third law: F_ij = - F_ji and τ_ij = - τ_ji)
- The sum of external torques.
Therefore, the total net torque is equal to the external net torque.



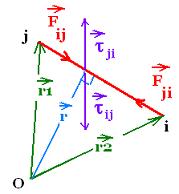
dL/dt = Στ_ext

Only external torques can change the angular momentum of a system. The torques and the angular momentum are measured about the same reference point in an inertial frame.

Recall an object rotates about a fixed axis. Its angular velocity ω and its moment of inertia are referred to an axis; whereas torque and angular momentum are both relative a refrence point.

3. Angular momentum of a rigid object

We want a relation between the moment of inertia relative to a fixed axis and the angular momentum of a rigid object with sufficient symetry relative to a point in this same axis.



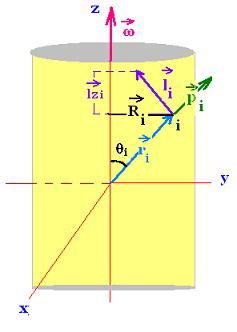
It we choose the z-axis (or axial) about the rigid object rotates, the component of the angular momentum of the object is L_z = Σl_iz. The z-comonent of the angular momentum of the particle i is l_i= r_i x p_i = m_iv_ir_i sin (r_i, v_i)
r_i and p_i are perpendicular, so:
l_i = m_iv_ir_i

Since v_i = ω_z R_i, and R_i = r_i sinθ_i we have then:
l_i = m_iω_z R_ir_i and l_iz= m_iω_z R_ir_isinθ_i = m_iω_z R_i²

l_i has both an axial and radial component. It doesn't depend of the location of the origin in the axis. Its expression is valid for any origin as long as the origin is on the axis.

Therefore:
L_z = Σl_iz = Σ m_iω_z R_i² = ω_z Σ m_i R_i² = ω_z I

L_z = I ω_z

I_z is the moment of inertia of the rigid object relative to the z-axis of rotation.

With an abject that has sufficient symetry, the radial components within the object cancel, so L is parallel to l_z. We have then:

L = I ω

3. Equation of motion for a rigid object
rotating about a fixed axis

Taking the time derivetive of the above equation giges: dL_z/dt = I dω_z/dt = I α_z But dL_z/dt = Στ_ext, so

Στ_ext = I α_z This the equation of motion of a rotating rigid object about a fixed z-axis.