Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
|
Rotational dynamics: Atwood's machine
1.Atwood's machine 3
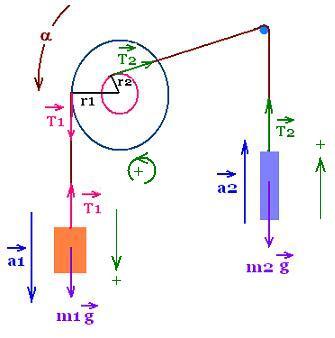
A pulley of moment of inertia I is made of two disks of
radii r1 and r2, welded together. The masses m1 and m2 are
attached to two strings, and each string is
wound around one of the disks as shown in the figure.
2. Second Newton's law for rotation
The second Newton's law for rotation for the pulley is:
τnet = Στ = I α (1)
That is :
T1 r1 - T2 r2 = I α (1')
α is the angular speed of the pulley. This
angular speed α is the same for the two disks
because they are attached to each other.
At the static equilibrium (for rotation and translation),
the angular speed is constant or zero (system at rest). Then:
α = dω/dt = 0. Therefore, the formula (1') becomes:
T1 r1 - T2 r2 = I 0 = 0, then
T1 r1 = T2 r2
The two torques τ1 = T1 r1 and τ2 = T2 r2 are
equal when the system is at rest or at constant speed.
The tangential acceleration "a1" for the disk 1 is
a1 = α r1 (2)
And
The tangential acceleration "a2" for the disk 2 is
a2 = α r2 (3)
3. Second Newton's law for translation
The second Newton's law for translation of the two masses is:
For m1:
m1 g - T1 = m1 a1 (4)
For m2:
- m2 g + T2 = m2 a2 (5)
From (4):
T1 = m1 g - m1 a1 = m1 (g - a1) (4')
From (5):
T2 = m2 g + m2 a2 = m2(g + a2) ( (5')
4. Solving for the tensions and accelerations
Multiplying (4') by r1 and (5') by r2, and
using the formula (1') yields:
T1 r1 - T2 r2 = r1 m1 (g - a1) - r2 m2(g + a2)
= I α
Using the relationships (2) and (3), we get:
T1 r1 - T2 r2 = r1 m1 (g - α r1) - r2 m2(g + α r2)
= I α
Developing:
T1 r1 - T2 r2 = r1 m1 g - α m1r12 - r2 m2 g - α m2r22
Rearranging to solve for α leads to:
r1 m1 g - r2 m2 g - α (m1r12 + m2r22) = I α
r1 m1 g - r2 m2 g = α (m1r12 + m2r22 + I)
Therefore:
α = (r1 m1 g - r2 m2 g)/(m1r12 + m2r22 + I)
We have then:
α = g(r1 m1 - r2 m2)/(m1r12 + m2r22 + I)
a1 = α r1
a2 = α r2
T1 = m1(g - a1)
T2 = m2(g + a2)
5. Applications
m1 = 3 kg, m2 = 1 kg
r1 = 10 cm , r2 = 5 cm
I = 0.20 kg.m2
g = 9.8 m/s2
α = 9.8(0.10 3 - 0.05 1)/(3 (0.10)2 + 1 (0.05)2 + 0.20) =
10.54 rad/s2
a1 = α r1 = 10.54 0.10 = 1.05 m/s2
a2 = α r2 = 10.54 0.05 = 0.53 m/s2
T1 = m1(g - a1) = 3(9.8 - 1.05) = 26.25 N
T2 = m2(g + a2) = 1 (9.8 + 0.53) = 10.33 N
For more details on the Atwood's machine,
go to:
AtWood's machine
|
|