Mechanics

1. Displacement:

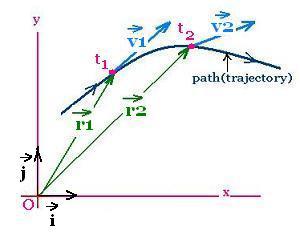
An object moves along the path from the left toward the right. In the reference frame xOy, its vector position is ⃗r₁at the time t₁, and ⃗r₂ at the time t₂. Then its displacement over the period of time Δt = t₂ - t₁ is Δ⃗r = ⃗r₂ - ⃗r₁. We can write:
⃗r₁ = x₁ ⃗i + y₁⃗j, and ⃗r₂= x₂ ⃗i + y₂⃗j
Then: Δ⃗r= [(x₂- x₁)⃗i + (y₂- y₁)⃗j

2. Velocity:

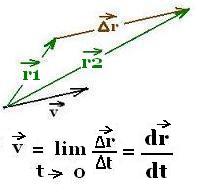
We will use three important terms relating to velocity.
The average velocity of the object is defined as the rate of the change of the displacement, that is ⃗v= Δ⃗r/Δt. Remark ⃗v and Δ⃗r are parallel and have the same direction (because they are two directly proportional vectors).

The instantaneous velocity or velocity for short is the limit of the average velocity when the measured period of time between two displacement is short. That is, if we assume t₁ fixed, and t₂ approaches t₁, Δt tends to zero. Thus, the average velocity becomes its derivative:

⃗v = lim (Δ⃗r/Δt) = d⃗r/dt
        Δt → 0

The speed is the magnitude of the velocity. In SI units, it is measured in meter per second (m/s or m s^-1).

Examples of speeds:
Our walking speed is about 1 m/s,
The speed of light is about 3 x 10⁸ ms^-1.

We can write:
⃗r = x ⃗i+ y ⃗j = d⃗r/dt = (dx /dt)⃗i+ (dy/dt)⃗j

3. Acceleration:

An acceleration is defined as the rate of the change of the velocity. That is:
⃗a = lim (Δ⃗v/Δt) = d⃗v/dt
        Δt → 0
Remark also ⃗a and Δ⃗v are parallel and have the same direction (because of their proportionality).

We have three cases depending on the related speeds (magnitude of velocities):

acceleration: when v2 > v1

Â

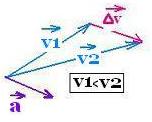
deceleration: when v2 < v1

Â

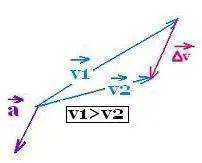
uniform motion: when v2 = v1

Â

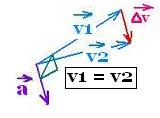
limit case: when dt tends to 0

In SI units, the magnitude of an acceleration is measured in meter per second (m/s/s or m/s² or m s^-2).



Example of acceleration:
The acceleration of gravity called gravitation is equal to about 9.8 m s^-2.

4. Expression of the acceleration in Cartesian coordinates:

We can write:
⃗r = x ⃗i+ y ⃗j

⃗v = v_x ⃗i+ v_y ⃗j
⃗v = (dx/dt) ⃗i+ (dy/dt) ⃗j

⃗a = (dv_x/dt) ⃗i+ (dv_y/dt) ⃗j
⃗a = (d²x/dt²) ⃗i+ (d²y/dt²) ⃗j
⃗a = (a_x/dt) ⃗i+ (a_y/dt) ⃗j
⃗a = d²âƒ—r/dt²

5. General motion: Expression of the acceleration in polar coordinates system:

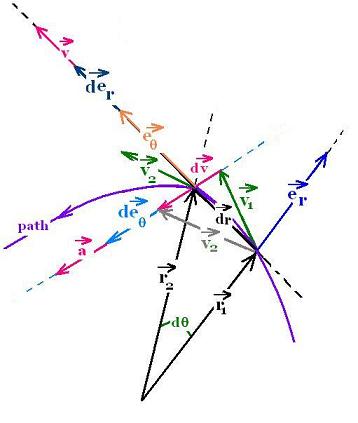At the time "t" the vector position is ⃗r1 and at "dt" after, it is ⃗r2; the resultant d⃗r as well as ⃗v (⃗v = d⃗r/dt) is tangent to the path along the vector unit ⃗eθ. The vectors d⃗rand ⃗eθ are colinear.

At the time "t", the velecity is ⃗v1 and at "dt" after, it is ⃗v2; the resultant d⃗v as well as ⃗a (⃗a = d⃗v/dt) is not tangent to the path. Its direction is
along a certain vector directed toward the center of curvature of the path. The acceleration vector can be decomposed to a component along the vector unit ⃗er (radial) and the second perpendicular vector unit ⃗eθ (tangential) .

Since the two vectors & #x20d7;er and ⃗eθ are orthogonal , we can write:
⃗eθ . ⃗er = 0
The derivative gives:
d⃗eθ . ⃗er + ⃗eθ . d⃗er = 0 , hence
d⃗eθ = - ⃗eθ . d⃗er/⃗er
The vectors ⃗eθ and d⃗er are collinear, thus
⃗eθ . d ⃗er = | d⃗er| . |⃗eθ| = der . eθ.
Therefore:
d⃗eθ = - eθ . der . ⃗er /er²
We have der = er . dθ, so
d⃗eθ = - eθ . er . dθ . ⃗er /er²
d⃗eθ = - (eθ/er) . dθ . ⃗er

d⃗eθ = - (eθ/er) . dθ . ⃗er (4.1)

Since eθ/er = 1/1 = 1 (the base {⃗er, ⃗eθ} is orthonormal), we have:

d⃗eθ = - dθ . ⃗er (4.2)

We have already set ⃗v = d⃗r/dt = (r dθ/dt)⃗ eθ.
Thus:
⃗a = d⃗v/dt = d[(r dθ/dt) ⃗eθ ]/dt
= (dr/dt) (dθ/dt)⃗ eθ + (r d²Î¸/dt²)⃗eθ + (r dθ/dt) d⃗eθ/dt =
= [(dr/dt) (dθ/dt) + (r d²Î¸/dt²)]⃗eθ + (r dθ/dt) d⃗eθ/dt

The third term becomes, according to the relationship (4.2):
(r dθ/dt) d⃗eθ/dt = - (r dθ/dt) (dθ/dt) ⃗er
Hence:
⃗a = [(dr/dt) (dθ/dt) + (r d²Î¸/dt²)]⃗eθ - (r dθ/dt) (dθ ⃗er)/dt =
[(dr/dt) (dθ/dt) + (r d²Î¸/dt²)]⃗eθ - r (dθ/dt)² ⃗er

⃗a = [(dr/dt) (dθ/dt) + (r d²Î¸/dt²)] ⃗eθ - [r (dθ/dt)²] ⃗er



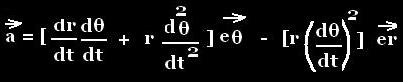
(component along ⃗ eθ + component along ⃗er)

The component:
⃗a_t = [(dr/dt) (dθ/dt) + (r d²Î¸/dt²)] ⃗eθ
Is the tangential acceleration.

The component:
⃗a_r = - [r(dθ/dt)²] ⃗er
Is the radial acceleration.

6. General motion: particular cases:

6.1. Circular motion:

The motion is circular when the related tarjectory is a circle; that is the vector position ⃗r is constant in magnitude "r". The expression of the acceleration becomes:
⃗a = [(r d²Î¸/dt²)] ⃗eθ - [r (dθ/dt)²] ⃗er

ω = dθ/dt is called angular velocity of unit rad/s.
α = dω/dt = d² θ/dt² is called angular acceleration of unit rad/s² .

The linear acceleleration ⃗a becomes then:

⃗a = r α⃗eθ - r ω² ⃗er

6.2. Uniform motion:

The motion is uniform when the angular velocity ⃗ω (then ⃗v) is constant in magnitude "omega;"; that is
dω/dt = d² θ/dt² = 0.
Therefore, the expression of the linear acceleration becomes:

⃗a = [(dr/dt) (dθ/dt) - [r (dθ/dt)²] ⃗er

6.3. Circular Uniform motion:

The two above cases, combined give the expression of the acceleration for a circular uniform motion:

⃗a = - [r (dθ/dt)²] ⃗er

A circular uniform motion (CUM) has just a radial component: a = r (dθ/dt)².
Since : || ⃗v|| = v = r (dθ/dt), we have: a = r (dθ/dt)² = r (v/r)² = v²/r

We define the period of revolution T in seconds for a CUM as the period of time that the oject takes to complete a cycle: ω = Δθ/Δt = 2π/T . The related frequency ƒ in s^-1 or Hertz is the number of cycles comleted per second: T = ƒ .

We have also the relationships between the angular and tangential velocities ω and v v = r dθ/dt = r ω. "r" is the radius of the circle.
ω = 2π/T = 2πƒ
v = r ω