Rotation
   Contents
   Applications
   Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2Ï€ rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Circular Uniform motion: applications
1. Circular Uniform motion CUM:
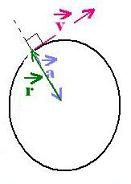The expression of the acceleration
for a circular uniform motion is:
⃗a = - [r (dθ/dt)2] ⃗er
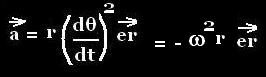
A circular uniform motion (CUM) has just a radial component:
a = r (dθ/dt)2.
Since : || ⃗v|| = v = r (dθ/dt), we have:
a = r (dθ/dt)2 = r (v/r)2 = v2/r
We define the period of revolution T in seconds for a CUM as the period of
time that the oject takes to complete a cycle:
ω = Δθ/Δt = 2π/T .
The related frequency Æ’ in s-1 or Hertz is the number of cycles
comleted per second: T = Æ’ .
We have also the relationships between the angular and tangential velocities ω and v
v = r dθ/dt = r ω. "r" is the radius of the circle.
ω = 2π/T = 2πƒ
v = ωr
2. CUM Applications:
2.1. Gravity function of altitude:
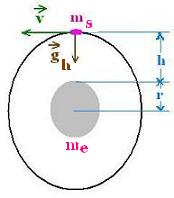The law of universal gravitation for the two objects (satellite and earth)
of mass ms and me (5.9742 × 1024 kg) respectively is written as:
F = G ms me / z2;
where G is the gravitational constant,
approximately equal to 6.673×10-11 N m2 kg-2, and "z" is the
distance betweem the two objects.
The distance "z", in this example is equal to the altitude of the satellite
above Earth "h" plus the Earth radius r = 6,357 km :
z = h + r
We assume that the motion of the satellite is circular and uniform. That
yields:
F = G ms me / z2 = ms gh,
where gh = g(z) is the acceleration of gravity at the distance
z = r + h.
When h = 0, g(z) becomes g(0) = g0 = 9.81 m s -2
(at Maryland). We have:
G ms me / z2 = ms gh
, so G me / z2 = gh. Then:
gh = G me / z2 = G me / (r + h)2
gh = G me / (r + h)2
gh = G me / (r + h)2
G me = 6.673×10-11 x 5.9742 × 1024 = 4.0 x 1014
g0 = g(0) = 4.0 x 1014 / (6,357.00 x 103)2
= 4.0 x 1014 / (6.357 x 106)2
= 4.0 x 1014 x 2.47 x 10-12 = 9.90 m s-2
2.2. Speed of a satellite:
If the satellite orbits at an altitude of 300 km, then:
gh = g(300 km) = 4.0 x 1014 / (6,357.00 + 300.00)2
= 4.0 x 1014 / (6.657 x 106)2
= 9.03 m s-2 (less than g0)
By equating the centripetal force ms v2/z on the satellite
and the weight ms gh of this object, we can write:
ms a = ms v2/z = ms gh.
The inertial mass in the centripetal force, and the gravitational mass in
the weight are equivalent, then:
v2/z = gh
v = [z x gh] 1/2 = [(r + h) x gh] 1/2
v (h) = [(r + h) gh] 1/2 = [G me / (r + h)] 1/2
v (h) = [(r + h) gh] 1/2 =
[G me / (r + h)] 1/2
This tangential speed does not depend on the mass of the orbiting object. It
is a function of the altitude h.
v = [(6,357.00 + 300.00) x 9.03 ] 1/2 = [(6.657) x 9.03 x 106] 1/2 =
[(6.657) x 9.03] 1/2 x 103 = 7.75 x 103 m.s-2.
For the moon, the altitude h is about 385,000 km, then:
v (h) = [(r + h) gh] 1/2 = [4.0 x 1014 / (6,357 + 385,000)x 103] 1/2
= [4.0 x 1014 / (3.91) x 108] 1/2 =
= [106] 1/2 = 10 3 = 1 km/s.
v(moon) = 1 km/s
According to ω = 2π/T, and v = z ω the period of the moon is T = 2π/ω =
2Ï€ z / v = 2Ï€ x 391,370 km / 1 km/s = 2Ï€ x 391,370 s = 682.72 hours = 28.45 days.
2.3. Escape speed:
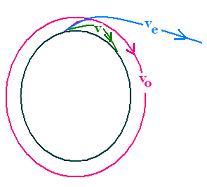Un object thrown upward falls, because it was launched with
a small speed, but with an escape speed, it will not fall. How much
does this speed be?
We assume that the origin of the potential energy is the earth surface. Then,
the potential energy of object to launch is Ep = - m g0 r
(m is the mass of the object, gp the acceleration of gravity at
the surface of Earth, and "r" is the radius of Earth.
At this position, the
object is thrown at the velocity ve, then its kinetic energy is
Ek = (1/2) m ve2.
The total energy of the object is
Et = Ep + Ek = - m g0 r +
(1/2) m ve2
Et = - m g0 r + (1/2) m ve2
If the object escapes, it will approach a place where its total energy is null.
As the total energy is conserved, Et = 0. That is:
- m g0 r + (1/2) m ve2 = 0. That yields:
g0 r = (1/2) ve2. Then:
ve = [2 g0 r]1/2
ve = [2 g0 r]1/2
ve = [2 g0 r]2 = [2 x 9.81 x 6,357 km]1/2
= 11.2 km/s
We have then three cases for an object of speed v :
- v < ve: The object falls.
- v = ve: The object orbits.
- v > ve: The object escapes.
2.4. Rounding corner:
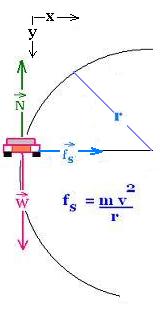A car rounds a corner od f radius r 50 m. The coefficient of static friction
between the tires and the road is μs = 0.80. There is a limit
for the speed of the car in the corner not to exceed to avoid skidding.
The three forces acting on the car:
Gravity, the normal force N and the force of static friction.
The force of static friction provides the centripetal
force required for the car to keep it moving in the circular path.
The greater the speed of the car, the more friction is needed.Hence:
mv2/r <= fs = μsN =
μsmg. That is:
v2/r <= μsg, or
v <= [μsgr]1/2
The speed limit is given by (independent of mass):
v = [μsgr]1/2
v = [μsgr]1/2
V = [0.80. 9.81.50]1/2 = 20 m/s
Remark:
The sum of the components of force gives:
Verically: Σ Fy = W - N = 0 or N = mg
Horizontally: Σ Fx = fs= μsmg = mv2/r
2.5. Banked Curves:
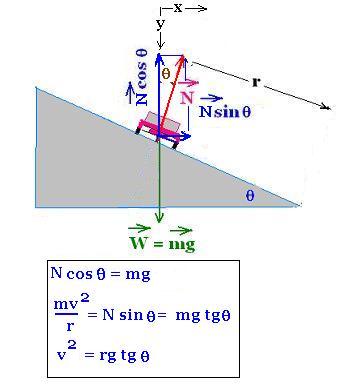Many roads are tilted or banked on corners by design.
On a banked curve, the required centripetal force is given by
the normal force N, that is the component
N sin θ..
Without no need to friction, we have the two forces W and N
acting on the car. The component N cosθ cancels the weight W:
Σ Fy = - N cos θ + W = 0, so
N cos θ = mg
And Σ Fx = N sinθ = m ax = mv2/r
Therefore, to remains in the circular motion:
mv2/r <= N sinθ = mg sinθ/N sinθ = mg tg θ
That is :
v <= [g r tg θ]1/2
The speed limit is :
v = [g r tg θ]1/2
v = [g r tg θ]1/2
For a car, witout a need to the friction force rounding
a corner in a circle of 80.0 m tilted at 45 o, the speed limit is:
v <= [9.81 . 80. 1 ]1/2 = 28 m/s
Earth radius: r = 6,357 km
Earth mass: me = 5.9742 × 1024 kilograms
Gravitational constant G = 6.673 × 10-11 N m2 kg-2
v(moon) = 1 km/s
g(0) = 9.81 m s-2
|
  |