Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Center of mass & collisions
1.Definitions
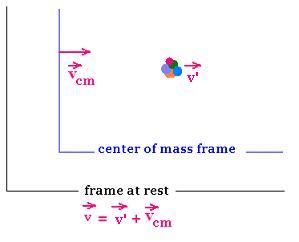
The velocity v of an object, or a particle i within this object,
in the frame at rest, is equal to the velocity of the center of mass (CM)
plus the volocity of this object or particle i in the frame of the CM, that is:
vi = v'i + vcm
The momentum of a particle "i" in the center of mass
frame is just its mass mi times its velocity v'i:
p'i = miv'i
In the CM:
vi = v'i + vcm
and
p'i = miv'i
2. Momentum in the CM frame
1. From the frame at rest
The momentum P of the object is:
Σ mivi.
2. From the frame of the CM
The momentum P' of the object is:
P' = Σmiv'i =
Σmi(vi - vcm) =
Σmivi - Σmivcm =
Σmivi - Mvcm) = P - P = 0.
We recall:
The sum of the momenta in the center of mass frame
is zero
Let's consider the collision:
(m1,v1) + (m2,v2) → (m1,w1) + (m2,w2)
in the frame at rest, and
(m1,v'1) + (m2,v'2) → (m1,w'1) + (m2,w'2)
in the CM frame, we have:
P' = Σpi = p'1 + p'2 = 0
Therefore:
p'1 = - p'2 before collision, and
q'1 = - q'2 after collision
The conservation of the kinetic energy gives:
p'12/2m1 + p'22/2m2
= q'12/2m1 + q'22/2m2
p'12/2 [1/m1 + 1/m2] =
q'12/2 [1/m1 + 1/m2]
(1/2) [1/m1 + 1/m2] [p'1 2 -
q'12] [1/m1 + 1/m2]
We have then two possibilities:
p'1 = + q'1 and
p'2 = + q'2
or
p'1 = - q'1 and
p'2 = - q'2
The first says that is no collision, and the second
shows that the momenta of both objects reverse their
directions. Since the masses do not change, we have for
the related velocities:
v'1 = - w'1 and
v'2 = - w'2
We recall:
In the center of mass frame of two objects, the
collision just reverses the direction of these two
objects.
We have;
vcm = [m1v1 +
m2 v2 ]/M
Then:
v'1 = v1 - vcm =
v1 - [m1v1 +
m2 v2 ]/M =
(1/M)[m1v1 +
m2v1 - m1v1
- m2 v2] =
(m2/M)[v1 - v2]
hence:
w'1 = -(m2/M)[v1 - v2]
Therefore:
w1 = w'1 + vcm
-v'1 + vcm = -v1 + 2vcm
w1 = -v1 + 2vcm
w2 = -v2 + 2vcm
w1 = -v1 + 2vcm
w2 = -v2 + 2vcm
That is:
w1 = v1(m1 - m2)/M + v2 2m2/M
w2 = v2(m2- m1)/M + v1 2m1/M
w1 = v1(m1 - m2)/M + 2v2 m2/M
w2 = v2(m2- m1)/M + 2v1 m1/M
3. Energy in the CM frame
P' = p'1 + p'2 = 0 before explosion
Q' = q'1 + q'2 = 0 after explosion
Before the explosion, the total energy of the object in the
center of mass frame is zero (because the original body was
at rest in this frame) After the explosion,
the total energy in this frame is:
ΔE = q'12 /2m1 + q'22/2m2 =
q'12 [1/2m1+ 1/2m2]
Therefore:
q'1 2= 2 m1m2ΔE/(m1 + m2)
Then:
w'2 = [q'22]1/2/m2 =
[2 m1ΔE/m2M]1/2
w'2 = [2 m1ΔE/m2M]1/2
Similarly,
m1 w'1 = - m2 w'2
Then:
w'1 = - m2 w'2/m1 =
- [2 m2ΔE/m1M]1/2
w'2 = [2 m1ΔE/m2M]1/2
w'1 = - [2 m2ΔE/m1M]1/2
w'2 = [2 m1ΔE/m2M]1/2
w'1 = - [2 m2ΔE/m1M]1/2
We have:
vcm = v
w1 = w'1 + vcm
w2 = w'2 + vcm
w1 = w'1 + vcm
w2 = w'2 + vcm
w1 = w'1 + vcm
w2 = w'2 + vcm
Etotal = (1/2)m1 w12 +
(1/2)m2 w12 =
m1 w12 = m1[w'1 + vcm]2
and
m2 w22 = m2[w'2 +
vcm]2,
According to: w'1 = - m2 w'2/m1, we have:
m2 w2 2 =
m2[(- m1w'1/m2) + vcm]2
m1[ 2 m1ΔE/m2M] + vcm]
Then:
m1 w12 + m2 w22 =
m1[ w'12 + vcm2 + 2w'1vcm] +
m2 [ (- m1w'1/m2)2 + vcm 2-
2 m1w'1/m2 vcm]
We have:
m1 2w'1vcm = m2 2 m1w'1/m2 vcm
Letting:
m1 w12 + m2 w22 =
m1[ w'12 + vcm2 ] +
m2 [ (- m1w'1/m2)2 + vcm2]
= m1 w'1 2 +
m2 w'222
+ (m1 + m2)vcm2 =
2ΔE + Mv2cm .
Etotal = ΔE + (1/2) Mvcm2
Etotal = ΔE + (1/2) Mvcm2
The total kinetic energy of a system is equal to the
kinetic energy of the center of mass plus the sum
of the kinetic energies of the objects of the sytem,
as calculated in the center of mass frame.
Other way to express directly the total energy
vi = vcm + v'i
Etotal = Σ (1/2)mivi2 =
Σ (1/2)mi(vcm + v'i)2 =
Σ (1/2)mi[vcm2 + v'i2+ 2 v'ivcm] =
(1/2) Σ mi[vcm2 + v'i2+ 2 v'ivcm]
We have:
(1/2) Σ mi2 v'ivcm
vcmΣ mi v'i = vcmΣ p'i = 0
Letting:
Etotal = (1/2) Σ miv2cm + (1/2) Σ miv'2i
= (1/2)M v2cm + (1/2) Σ miv'2i
= Ecm + E'
Etotal = Ecm + E'
4. Example:
For the head-on collision in the rest frame:
(m,V) + (M,0) &arra; m w1+ Mw2, we
have:
w = 2m/(m+M)
w'2 = w2 - vcm
vcm = mV/(m + M), so
w'2 = w2 - mV/(m + M) = mV/(m + M)
Therefore:
w'22 = m2V2/(m + M)2
= 2mΔE /M(m + M), so
ΔE = (1/2) m V2 M/(m + M)
If K is the kinetic energy = (1/2) mV2 of the
projectile (m,V), we have:
ΔE = K M/(m + M)
Collision: (m,V) + (M,0)
The enrgy available to cause reaction is
ΔE = K M/(m + M)
Collision: (m,V) + (M,0)
The energy available to cause reaction is:
ΔE = K M/(m + M)
K is the projectile's kinetic energy = (1/2) mV2
|
|