Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Force and torque on a current loop
Let's consider a current-carrying conductor that forms
a loop of radius r within a uniform magnetic field B. The loop
is a series of straight line segments. In each segment, according
to the right-hand rule, a force has an opposite in the other side.
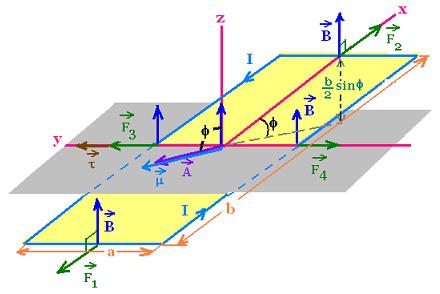
F3 = F4 = BIb sin(π/2 - φ) = BIb cos φ.
Their sum is zero and they produce no torque.
F1 = F2 = I B x a = IBa. They are not along the same line
of action. Their sum is not zero and they produce a torque of
F x (b/2) sin φ each. The right-hand rule shows that the two
produced torques are directef toward +y-axis. The net vector torque
produced by the two force F1 and F2 is:
τ = 2 F x (b/2) sin φ = F b sin φ = IB a b sin φ
Since ab = A, that is the area of the loop, the magnitude of the
torque becomes:
τ = IB A sin φ
Using the vector area A = A . (normal vector to the area ab), so
the angle φ is the angle between the vector B and the vector A,
we have the following cross product:
τ = I B x A
The product IA is called the magnetic dipole moment or
magnetic moment of the loop and written as μ so:
μ = I A
Using this formula, yields:
τ = μ x B
(Remark that we used here a property of cross product
a x b = - b x a. The angle here is betwen the vector A (or μ)
and the vector B).
τ = μ x B = τ = μ B sin φ. When φ = 0
the torque is zero and the normal to the loop is parallel to
the field; that corresponds to the stable equilibrium position.
When φ 2π, the torque is zero and the
normal to the loop is antiparallel to the field; that correspond to
the unstable equilibrium position. The torque is at its
maximum at φ = π/2, when μ and B are perpendicular.
The torque tends to bring back the loop to its stable
equilibrium position.
When a magnetic dipole changes orientation in a magnetic
field, the magnetic field does work on it. This work
corresponds to a potential energy U = - μ . B = - μ B cos φ.
U = - μ . B = - μ B cos φ
This results found for a rectangular current loop are
valid for any a plane loop of any shape. For a solenoid
of N planar loops close together, just multiply the current
I by N and apply the related formulas.
|
|