Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Motion of a gyroscope
There are two external forces acting on the system:
the weight W = Mg of the flywheel and its reaction R
on the pivot. We will choose this pivot as the
reference point for torques. The torque of the reaction
R is zero since R is along the axial z-axis. The net
torque is then the one created by the weight w,
so Στ = net torque = r x w. The related total angular
momentum (always in the same direction as the net torque
τ) is given by the formula:
τ = dL/dt
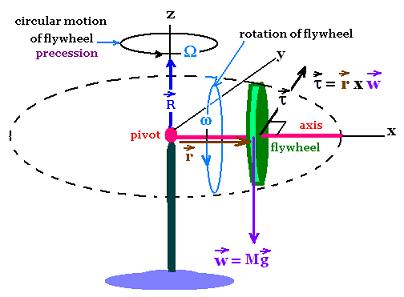
1. Flywheel not spinning
When the flywheel does't spin, Li = 0. The variation dL
of the system produced by the torque remains in the initial direction
and form the final angular momentum Lf = Σ dLi.
The flywheel fulls and stops at a certain time. (figure a)
2. Flywheel spinning
The flywheel starts to spin at a constant angular speed ω =
ωs about x-axis. The related initial angular momentum
is Li = Ls, which is the spinning angular momentum
of the flywheel. When the flywheel is released, at a short time dt, the
torque τ w x r = Mg x r gives rise to dL. dL
and τ stay parallel in the plane (x,y). Their resultant
poduces a new angular momentum L = dl + Li. Hence the flywheel
is shifted to spin about the rotated x-axis along the resultant
angular momentum L = dl + Li.
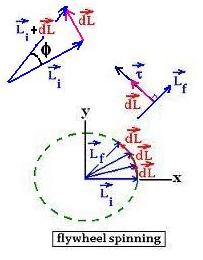
Since dL and L are
always perpendicular, the dispalcement of all dL will be along
a circle of radius r. Hence, Li and all Li + ΣdL
that is Lf are equal in magnitude, but not in direction.
Therefore, the rotation of Lf about the axial z-axis
gives rise to the angular momentum Lp of angular velocity
Ω about the axial z-axis. Lf spins and rotates
around the axial of vector unit k in the plane (x,y), we can
then write Lf = Ls i + dl j. The rusultant
Lr of Ls, dL and Lf is written as:
Lr = Ls i + dL j + Lp k.
Lr = Ls i + dL j + Lp k
In a gyroscopic motion systems like a flywheel, the angular velocity
ωp is much smallar the the spinning angular velocity
ωs (ωp <<ωs),
so the resultant Lr becomes Lr = Ls i + dL j,
that is Lp; Lp = Ls i + dL j.
Lp = Ls i + dL j
The rotation associated to Lp is called
precession.
3. Expression of precession angular speed
The equation τ = dL/dt gives
r x w = Mg r = dL/dt, then;
dL/dt = Ls dφ/dt = Ls ωp = Mgr
Since Ls = Is ωs, where Is
is the moment of inertia of the spinning flywheel, we can write:
ωp = Mgr/Ls = Mgr/Is ωs
R is the distance between the axial z-axis to the center (of
mass) of the flywheel.
Precession: ωp = Mgr/Is ωs
Remark that the precession angular speed ωp becomes larger
when the spinning ωs weakens. This is what happens
at the end when friction reduces the rotation of Lr .
If the flywheel is considered as a solid cylinder of moment of
inertia Icm = Is = (1/2) M Ro2, the above
expresion becomes:
ωp = Mgr/(1/2) M Ro2 ωs =
2gr/Ro2 ωs.
ωp = 2gr/ωsRo2
That is independent of the mass of the flywheel.
Finally, note that the change in the positin vector r
exhibits a nutational motion producing a
translation of the wheel while spinning, along its axis (x-axis).
|
|