Rotational kinetic energy: Momemnt of inertia

1. Rotational kinetic energy

When an object rotates, the rotation gives it a kinetic energy. 

Let's consider a rotating rigid object. Each particle "i" of this 
object rotates at the same angular velocity ω = vi/ri. 
Where vi is the tangential (linear) velocity of the particle "i" 
localized by the radius ri from the rotation-axis.

The kinetic energy of the particle "i" is Ki = (1/2)mivi2 = 
(1/2)miω2ri2 = (1/2) ω2 mir2i 

For the whole rigid body, we have: 

K = Σ Ki = (1/2) ω2 Σ miri2

Σ miri2 is called the moment of inertia denoted by I.
Therefore:

K = (1/2) I ω2 

I = Σ miri2 

2. Momemnt of inertia

The momment of inertia is not an intrinsic property 
of a system. This is an example:


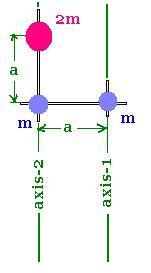I( relative to axis-2) = ma2
I( relative to axis-1) = ma2 + 2ma2  = 3ma2 

The momment of inertia depends on the mass of the systembut mainly on 
the distribution of mass perpendicular to the rotationa axis.

For a continuous object, we express first the mass in terms of volume by 
mass (m) = ρ x volume (V), and write: 

I = ∫ r2 dm  = ∫ ρ r2 dV 

We consider an unifrm density, hence:


I = ∫ r2 dm  = ρ ∫ r2 dV 
(integral over the volume V)

3. Parallel axis theorem

The momemnt of inertia changes regarding a choice of 
an axis of rotation.



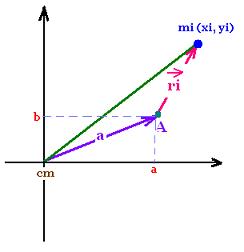In this choice the coordinates of the center of mass 
are null xcm = ycm = 0

The point A is in the (x,y) plan. The z rotational axis 
is out of the page.

The moment of inertia of the rigid body relative to the axis 
crossing the center of mass (CM) is:


Icm = Σmi (xi2 + yi2)


The moment of inertia of the rigid body relative to the axis 
passing across the point A, distant of d from the CM is:

IA = Σmi ri2 = Σmi [(xi - a)2 + (yi - b)2 ] = 

Σmi [(xi2 + a2 - 2 axi) + (yi2 + b2 - 2 ayi) ] = 

Σmi [(xi2 + yi2 a2 + b2 - 2 axi) +  2 ayi) ] =

Σmi (xi2 + yi2) + Σmi (a2 + b2) - 2 a Σmixi) +  2 aΣmiyi) ]

Since :
Σmixi = M xcm = 0
Σmiyxi = M ycm = 0
Icm = Σmi (xi2 + yi2)
a2 + b2 = d2
Σmi = M


We have then:
IA  = Σmi (xi2 + yi2) + M d2

 Parallel axis theorem:

IA = Icm + M d2


Example: Uniform thin rod of length L



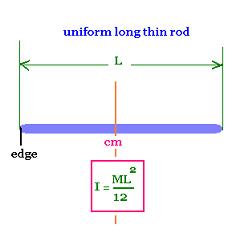The center of has the following coordinates:
xcm = 0
ycm  = L/2

Icm = ∫ x2 dm = ∫ x2 ρ  π R2 dx = ρ π R2 ∫ x2 dx  

From - L/2 to + L/2 
=  ρ π R2 x [(L/2)3 /3 - (-L/2)3 /3] = 
=  ρ π R2 /3  x [(L3/8) - (- L3/8]
=  ρ π R2 /3  x  (L3/4) = 
ρ V  x  (L2/12)  = M L2/12


Rod Moment of Inertia:
Icm = M L2/12


Now the moment of inertia from the axis passing through 
the left edge, according to the parallel axis theorem :

Iedge = M L2/12 + M (L/2)2 = 4 M L2/12 =  M L2/4