Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
|
Rigid Rotor
1. Reduced mass
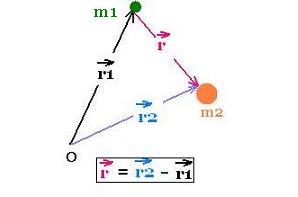
From any arigin O in an inertial frame at rest, the vector
positions of the particles of mass
m1 and m2 are r1 and
r2 respectively.
The vector position of
the center of mass of the two particles is: rcm =
(m1 r1 + m2r2)/M.;
where M = m1 + m2.
Now, we choose the origin O as the CM of the system
of the two particles, so rcm = 0. Therefore:
m1 r1 + m2r2 = 0
r1 and r2 are then collinear.
Hence:
r1 = - (m2/M) r , and
r2 = + (m1/M) r
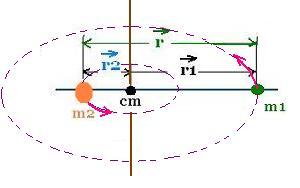
The moment of inertia of the system in the CM frame is:
Icm = m1r12 + m2r22 =
m1 x m22 r2/M2 +
m2 x m12 r2/M2 =
(m1m2/(m1 + m2) r2
The ratio: μ = m1m2/(m1 + m2) is called the reduced mass of the
system of two particles.
Reduced mass of the system of two particles:
μ = m1m2/(m1 + m2)
The moment of inertia of the system in the center
of mass CM is then:
Icm = μ r2
r is the distance between the two particles.
Moment of inertia of the system of two particles in the center
of mass CM :
Icm = μ r2
r is the distance between the two particles.
2. Energy of a rigid rotor
The classical rotational kinetic energy of this rigid object
is E = (1/2) I ω2, that is associated with
he rotational angular momentum L = I ω. So;
E = (1/2) I (L/I)2 = L2/2I
Using the equation of Schrodinger, we have:
Hψ = E ψ = (L2/2I)ψ = [J(J + 1)ħ2/2I ]ψ
Therefore, by using the eigenvalues of the angular momentum operator L, we find the energy levels for the rigid rotor:
E = J(J + 1)ħ2/2I
Icm = μ r2
E = J(J + 1)ħ2/2I
μ = m1m2/(m1 + m2).
J is the orbital quantum number = 0, 1, 2, 3, ...
These results are applied mostly for diatomic molecules,
such as HCl, NaCl, NaI, KCl ans so on.
|
|