Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
|
Rolling objects
1. Rolling objects
A rigid object that translates and rotates is said that
it rolls. If it rotates about a fixed axis and moves without
sliding along a straight line, the axis of rotation translates
with a fixed orientation.
For an object that rolls without sliding, there is a relationship between the
linear speed v of its center and the rotational speed ω about
an axis through its center.
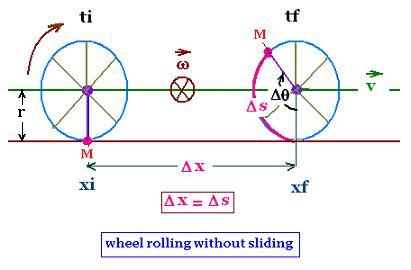
For a rolling wheel of radius r without sliding, the center of the wheel (axle) moves the
distance Δx from the point xi fo the point xf, at a speed v, in a period of
time Δt = tf - ti, while the point of contact M moves along the edge (rim) of the wheel
the distance Δs equal to Δx.
Therefore:
v = Δx/Δt = Δs/Δt = r Δt/Δt = r ω
Rolling without sliding:
v = r ω
1. Total kinetic energy of a rolling object
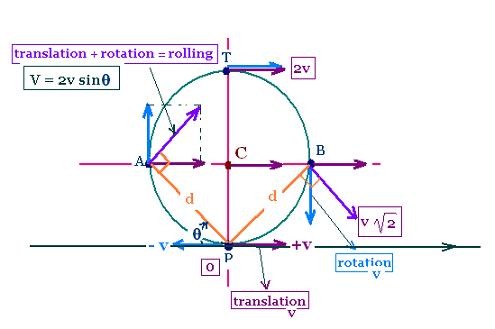 Any point (particle) in the edge of the rotating wheel,
rotates about an axis through the point of contact P which is
not fixed but moving at the speed v.
Any point (particle) in the edge of the rotating wheel,
rotates about an axis through the point of contact P which is
not fixed but moving at the speed v.
At a any time, the linear speed
of the point of contact P is zero. The linear velocity v of each
particle (point) on the edge of the wheel is equal to d ω, where
d is the distance between the point of contact P and the particle (point),
and ω is the angular speed of the wheel. The maximum speed is the
one of the top of the wheel T: v = 2rω. This linear speed
is tangential, thus perpendicular to the distance d.
Each point (particle) of the edge has two linear velocities: the
first is due to a pure translation at the speed v of the whell (including its
center), constant in magnitude and direction. The second is due to
a pure rotation of the wheel about the axis through its center, constant in
magnitude and changing in direction *omega;d = v.
Each time, we have V = vt + vr = v i + v j. The unit vector
i is constant, whereas the unit vector j rotates and makes a cycle. Hence:
For the point P (at the bottom): V = v i - v i = 0
For the point A: V = v 21/2
For the point T (at the top): V = 2v
For the point B: V = v 21/2 as for the point A
For again the point P (at the bottom): V = v i - v i = 0
The linear speed of the rolling object can be expressed by:
V = 2 v sin θ
Where θ i sthe angle the horizontal and tyhe vector
rotational velocity.
Since d = 2r sinθ thus:
V = v d/R
The vector linear velocity V is at each time perpendicular to
the distance d and its magnitude varies with respect to d
Linear speed of rolling object:
V = 2 v sin θ = v d/r
v is the linear speed of translation:
The angular speed ωp about the axis through the
contact point P is the same as the angular speed ωc about
an axis through the center C of the rolling object, henec
ωc = ωp = ω = v/r
3. Total kinetic energy of a rolling object
The total kinetic energy og the rolling object relative to
the point of contact P is:
K = (1/2) IPω2
Where
IP = Icm = C + M r2
is the moment of inertia of the rolling object about
an axis perpendicular to the direction of motion through p.
M is the mass of the rolling object.
According to the parallel-axis theorem, wehave:
K = (1/2) (IC + M r2) ω2 =
(1/2) ICω2 + (1/2) M r2ω2
Since (1/2) M r2ω2 = (1/2) M (rω)2 =
(1/2) M v2
Therefore:
K = (1/2) Icmω2 + (1/2) M v2
Total kinetic energy f the rolling object:
K = (1/2) Icmω2 + (1/2) M v2
The kinetic energy of a rolling rigid object is the
sum of two terms: the rotational kinetic energy (1/2) Icmω2
of the center of mass, and the translational energy (1/2) M v2
of the center of mass.
|
|