Rolling motion: Bicycle
different cases for the wheel
1. Wheel at rest
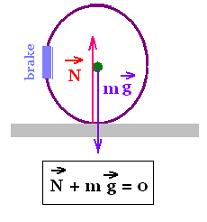
Along a vertical axis, we have:
N + mg = 0
2. Motion of the wheel with sliding effect
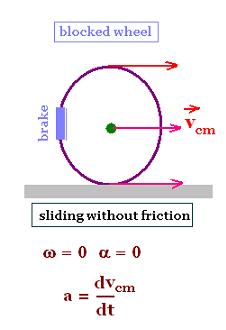
The whell slides witout friction as it does a bicycle
when it is sliding on ice. This is the case of a simple block that
slides along a frictionless path.
All the parts of the whell has the same linear
velocity vcm. The angular velocity
ω is zero, so is the angular acceleration.
With some external force, the whell will
undergo a linear acceleration a = dvcm/dt.
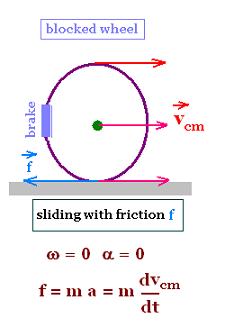
The whell slides with friction as it does a bicycle
when it is moving and braked all of a sudden, or as it does an erasing
rubber on a paper. This is the case of a simple block that slides
along a path with kinetic friction.
All the parts of the whell has the same linear
velocity vcm. The angular velocity
ω is zero, so is the angular acceleration.
The external force acting on the wheel is the friction force ƒ
providing the whell a linear decceleration a = dvcm/dt.
Along a horizontal axis, we have :
- ƒ + ma = 0 or ƒ = ma
Along a vertical axis, we have :
N = m g
Therefore:
ƒ = μk N = μk m g
ƒ = μk N = μk m g = m a
a = μk g
3. Rotation of a free wheel
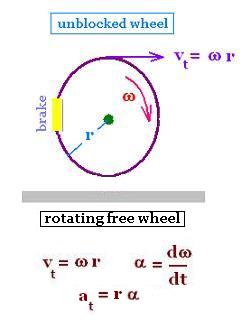
The wheel rotates freely about its axis located
at the center of the wheel.
Its angular velocity
ω is related to a tangential speed v as: v = ω r, where
r is the radius of the whell.
The translation motion of the wheel is zero.
Therefore:
a = d/vcmdt = 0
a = d/vcmdt = 0
vt = ω r
α = dω/dt
at = r α
4. Frictionless rotating wheel
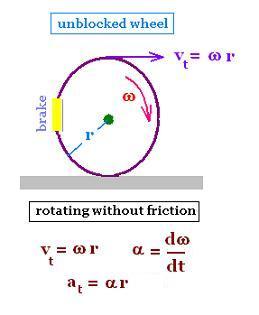
The frictionless wheel rotates and slides about its axis located
at the center of the wheel. The wheel floats on its support, as on ice.
Its angular velocity
ω is related to a tangential speed v as: v = ω r, where
r is the radius of the whell.
The rotating motion of the wheel will remain uniforme (ω = constant) unless
a torque is exerted on it and provides it an angular acceleration.
vt = ω r
α = dω/dt
at = r α
5. Friction rotating wheel
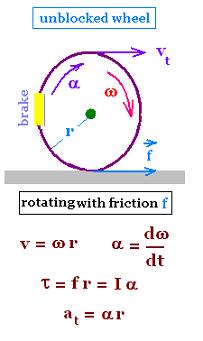
The wheel rotates with a kinetic friction about its axis located
at its center, as it does a rotating sharpening tool when we hold someting against its
grindstone.
Its angular velocity
ω is related to a tangential speed v as: v = ω r, where
r is the radius of the whell.
Its angular acceleration α has the expression:
α = dω/dt.
Related to the torque due
to the friction force ƒ , we have:
τnet = ƒ r =I α
,
where I is the moment of inertia of the wheel.
6. Rolling and slading frictionless wheel
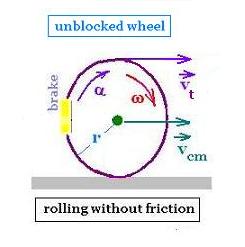
7. Rolling and slading wheel with friction
8. Rolling frictionless wheel
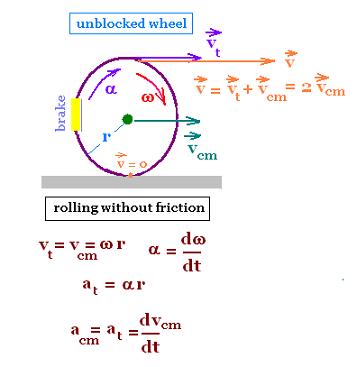
The wheel rolls (translates and rotates) without friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
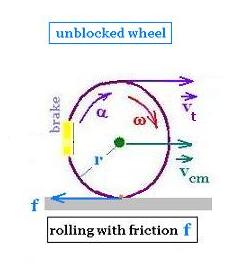
9. Rolling wheel with friction
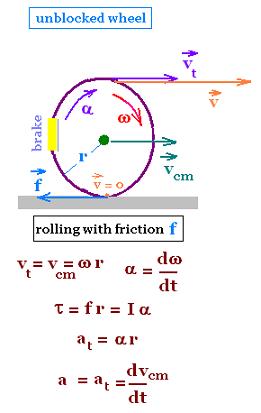
The wheel rolls (translates and rotates) with friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
Related to the torque due
to the friction force ƒ , we have:
τnet = ƒ r = I α
,
where I is the moment of inertia of the wheel.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = ƒ r = I α
10. Rolling braked frictionless wheel
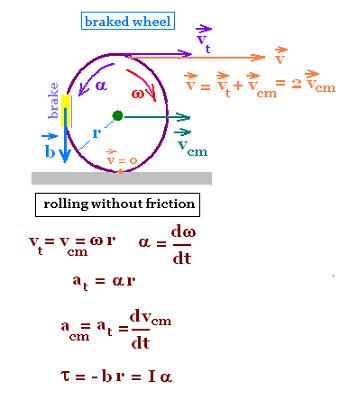
The wheel rolls (translates and rotates) without friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
Related to the torque due
to the brake force b , we have:
τnet = - b r = I α
,
where I is the moment of inertia of the wheel.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = - b r = I α
11. Rolling braked wheel with friction
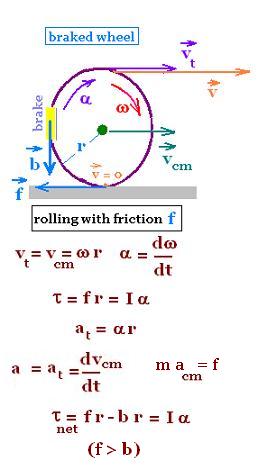
The wheel rolls (translates and rotates) with friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
Related to the two torques due
to friction force ƒ and the brake force b , we have:
τnet = ƒ r - b r = I α
,
where I is the moment of inertia of the wheel.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = ƒ r - b r = I α
To be slowed by friction: ƒ r < b r .
12. Rolling pulled frictionless wheel
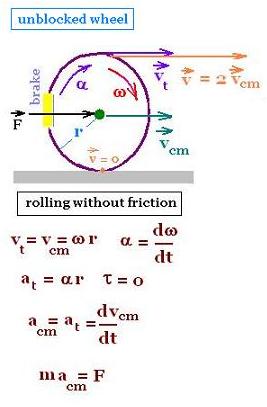
The wheel rolls (translates and rotates) without friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt,
with
F = m acm, m is the mass of the wheel.
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
F = m acm
13. Rolling pushed wheel with friction
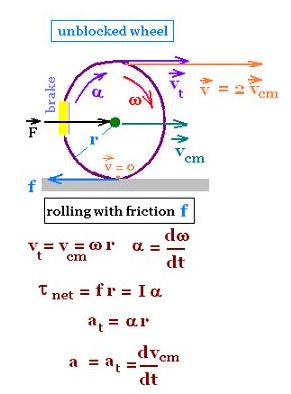
The wheel rolls (translates and rotates) without friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt. Related to the torque due
to the static friction force ƒ, we have:
τnet = ƒ r = I α
,
where I is the moment of inertia of the wheel.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt,
with
F = m acm, m is the mass of the wheel.
F is responsible for acm, and
ƒ is pesponsible for α
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = ƒ r = I &alpha
F = m acm
14. Rolling frictionless wheel with tension on the sprocket
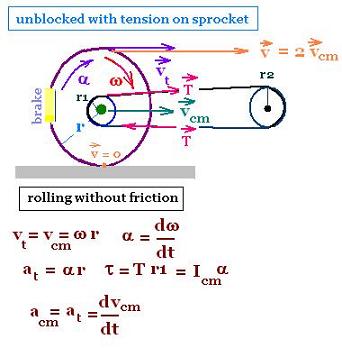
The wheel rolls (translates and rotates) without friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt.
Related to the torque due
to the tension force T , we have:
τnet = T r1 = I α
,
where I is the moment of inertia of the wheel, and
r1 is the radius of the sprocket.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt,
The tension T is pesponsible for α
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = T r1 = I α
15. Rolling wheel with tension on the sprocket and friction
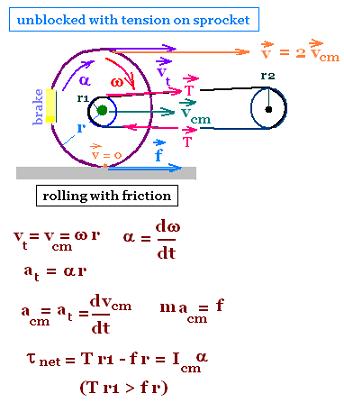
The wheel rolls (translates and rotates) with friction. It translates along its
center of mass which is its center. Plus, it rotates about its axis located
at this center.
Its angular velocity ω is related to a tangential speed vt
as:
vt= ω r,
where
r is the radius of the whell.
We have also:
vt = vcm
The relative speed v at the top of the wheel v is the linear sum
of vt and vcm
v = vt + vcm = 2 vcm.
Its angular acceleration α has the expression:
α = dω/dt. Related to the two torques due
to the friction force ƒ and the tension on the sprocket
provided by a pedalling system, we have:
τnet = T r - ƒ r = I α
,
where I is the moment of inertia of the wheel.
And its tangential acceleration is equal to its linear
acceleration:
a = at = acm = dvcm/dt,
The tension T is pesponsible for α, and
The friction ƒ , by the torque ƒ r, is pesponsible for α.
vt= ω r
vt = vcm
v = vt + vcm = 2 vcm
a = at = acm = dvcm/dt = α r
τnet = T r - ƒ r = I α
We would have T r > ƒ r to move on.
16. Acceleration of a bicycle
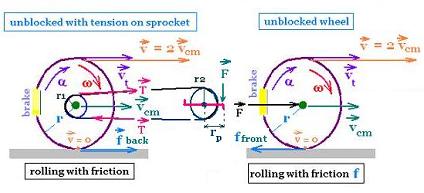
We have the following relationships:
F rp = T r2 (1)
T r1 - ƒback r = I α (2)
(F rp/r2) r1 - ƒback r = I α (3)
(F rp r1/r2) - ƒback r = I α (4)
Fnet = ƒback - ƒfront = m a = m r (5)
m is the mass of the bicycle and a is its linear or tangential
acceleration.
α is the angular acceleration of the back as well as
of the front wheel. We assume that the two wheels have approximately
the same moment of inertia I.
ƒfront r = I α (6)
Therefore:
(5) becomes:
ƒback r - I α = m a = m r2 α(5)
With (3)
(F rp/r2) r1 - 2I α = m r2 α(5)
(F rpr1/r2) = 2I α + m r2 α(5)
(F rpr1/r2) = (2I + m r2) α(5)
α = (F rpr1/r2) /(2I + m r2)
a = ( r F rpr1/r2) /(2I + m r2)
a = ( r F rpr1/r2) /(2I + m r2)
|

