Rotational kinematics
1. Introduction
A pulley, on its axle, rotates. A door turns on its hinges. A wheel of a bicycle rolls,
that is it rotates and translates. The planet earth spins about
its axis once a day and orbits the sun once a year.
In a translational
motion, each particle of a rigid body has the same linear velocity.
In a rotational motion about an axis, each particle of a rigid body has a same the same
angular velocity, but not the same tangential linear velocity.
2. Angular measurements
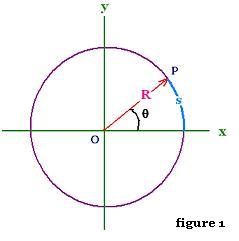The convenient unit to use for rotational motion to measure angles is
the SI unit, the radian (rad). In figure 1, the angle
θ in radian is defined as the ratio s/R, where s the arc
from the x-axis to the line segement OP, and
R is the radial distance from O to M; both meseared in the same unit of length.
θ = s/R
For a full circle s is the circumference of the cercle, that is
s = 2πR; then θcircle = 2πR/R = 2π rad.
Meaurements in degrees and revolution give:
2π rad = 360o. Thus 1 rad = 360/2π ≈ 57.3 o
1 rad ≈ 57.3 o
Another way to measure angles is revolution (rev). Revolution
corresponds to a full rotation or a cycle.
Then: 1 rev = 360o = 2π rad. This unit is often
used with the angular spped to measure it in radins/minute (rad/min).
Remark that an angle has not unit since it is a ratio of lengths, so
the used units rad, do and rev are written
with a mesurement in order to be convenient only.
3. Angular velocity and acceleration
The angular quantities: angular coordinate θ, angular velocity ω;
and angular acceleration α are mathematically similar to those of
of a linear motion.
3.1. Angular coordinate
The rotation of the object about
the fixed axis z-axiz in figure 2, viewed from above (+z-axis)
is counterclockwise and positive. Conversely, it will be
clockwise and negative. Note that the angular coordinate
θ is cyclic, that is θ and θ + n(2π) have
the same angular positions ( n is any positive or negative integer).
A right-hand rule gives the direction of
its progression (curling fingers), and then the direction (thumb points to +z)
of the angular velocity ω.
3.2. Angular velocity and angular speed
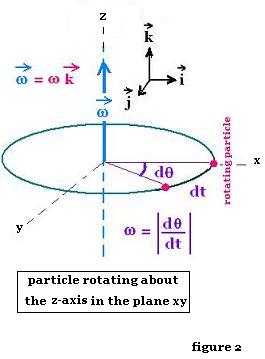The angular speed is the magnitude of the vector angular velocity;
that is its absolute value. The velocity is the rate in
change of the angular coordinate: ω = |dθ/dt|
If the object rotates about another axis other than z-axis,
the plane of its rotation stays always perpendicular to
its axis of rotation, and the angular velocity will have three
components. Therefore along the chosen z-axis,
ω = ωz k.
For a particle circling the axis of rotation z,
the vector ω is perpendicual to the plane of motion xy.
ω = ωz k
ωz = dθ/dt
The angular coordinate is dimensionless and its unit is the
radian (rad). Therefore the angular velocity has the dimention of
1/time and its unit is the radian per second (rad/sec).
3.3. Angular acceleration
When the angular velocity of a rotating bject (or particle) changes,
as if the an object starts to rotates or is about to stop, the rate of
this change provides an acceleration for the object (or particle).
This acceleration α is a vector that has the same direction as
the vector angular velocity ω (along the axis of rotation).
Similarly as ωz, we have α = αz k.
αz = dωz/dt = d2θ/dt2
α is negative when ω decreases, and positive
when ω increases. The magnitude of the angular acceleration
has the dimension of time-2 and its unit is the radian
per second2 (rad s- 2).
4. Kinematics of rotation about a fixed axis
4.1.Constant angular velocity
From the relation ωz = dθ/dt, we have
when the angular velocity ωz is constant:
θ = ωz t + θ0. If
at t = 0, we have θ = 0, so θ0 = 0
and: θ = ωz t .
θ(t) = ωz t + θ0
4.2. Constant angular acceleration
From the relation αz = dωz/dt, we have
when the angular acceleration αz is constant:
ωz = αz t + ωz0. If
at t = 0, we have ωz = 0, so ωz0 = 0
and: ωz = αz t .
ωz(t) = αz t + ωz0
We have: dθ/dt = ωz(t) = αz t + ωz0
integrating from an initial time zero to a final time t will give
the expression of the angular position θ(t).
From the relationship found above: ωz(t) = αz t + ωz0,
we have:
θ - θ0 = ωz(t - t0) =
(1/2) αz t2 + ωz0 t.
α(t) = (1/2) αz t2 + ωz0 t + θ0
By eliminating the time t between the two above equations, we obtain:
t = [ωz - ωz0]/ αz, and then:
θ(t) - θ0 = (1/2) αz ([ωz(t) - ωz0] /αz)2 + ωz0 ([ωz(t) - ωz0] /αz)
We find:
2αz (θ - θ0) = ωz2 - ωz02
ωz2 - ωz02 = 2αz (θ - θ0)
4.3. Example:
The angular speed of a wheel decreases from 90 rad/s untill
it stopped in 10 seconds. We want to calculate:
a) The angular acceleration of this wheel, and
b) The related angle displacement.
a)
ωi = ωo + α ti = 90 rad/s
ωf = ωo + α tf = 0
Subtracting yields:
ωf - ωi = α (tf - ti) = - 90 rad/s
Therefore:
α = (0 - 90) /(10 - 0) rad/s/s = - 9 rad/s2
α = - 9 rad/s2
b)
θ(t) = θo + ωot + (1/2) αt2 =
θ(t) = 0 + (90 rad/s) (10 s) - (1/2) (9 rad/s2) (10 s) 2 =
900 - 450 = 450 radians = 71 x 2π + 0.62 x 2π =
= 71 cycles + 4 radians = 71 cycles + 4 (180/π) = 71 cycles + 229o
5. Linear and angular velocity and acceleration
An object that moves from an angle θi at ti
to an angle θf has average angular speed
ω = (θ f - θ i)/(tf - ti) = Δθ/Δt.
Instantaneous angular speed is obtained by taking Δt small,
and write:
ω = dθ/dt = lim Δθ/Δt
when Δt tends to dt.
let's consider the following circular moton:
We have dr = r dθ
The velocity is:
v = dr/dt = r dθ/dt = r ω
The acceleration is:
a = dv/dt = (dr/dt) (dθ/dt) + r (dθ2/dt2)
a = v ω + r α
= ar + at
ar = v ω = r ω2 = v2/r
at = r α
a is the he linear acceleration, and
ar its radial acceleration, and
at its tangential acceleration.
There is no radial velocity. The velocity is tangential since
the motion is circular : v = vt = r ωz = r ω.
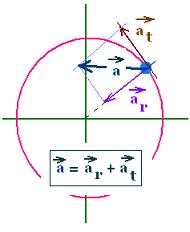
Circular motion:
a = ar + at
radial acceleration
ar = v ω = r ω2 = v2/r
tengential acceleration
at = r α
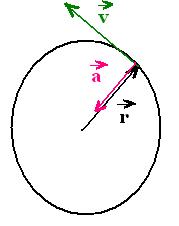
If the motion is uniform, we have dv/dt = dω/dt = α = 0;
letting just a radial acceleration and called centripetal acceleration.
|