Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Rotational work and power for rigid object
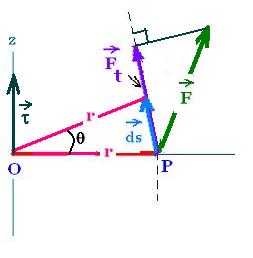
1. rotational work
When a force causes a torque by rotating an object, the agent
that exerted this force does a work. If the agent rotates the
object by an angle dθ, during a time interval dt; the work done by the force F is:
dW = F . ds = F ds cos θ = F cos θ ds =
Ft ds = Ft r dθ = τ dθ
Where Ft is the tangential component of the force F,
and τ = r Ft
This torque is the net torque. That is
the sum of all the torques in the object τ = Σ τi.
The net work done by this torque rotating the object OP
from an angle θi to an angle θf is:
Wnet = ∫ τ dθ
From θi to θf
If the torque τ is constant, we will have:
Wnet = τ (θf - θf)
The general case is:
W net= ∫ τ dθ = ∫ I α dθ
From θi to θf
Where I is the moment of inertia of the object.
Since α = dθ2/dt2 = dω/dt and
ω = dθ/dt
Then:
α dθ = (dω/dt) dθ = dω (dθ/dt) = dω ω
Therefore:
Wnet = I (dθ/dt) = I ∫ dω ω =
From ωi to ωf
= (1/2) I (ωf2 - ωi2)
Work done by a torque on a rigid object :
Wnet = (1/2) I (ωf2 - ωi2)
2. Power delivered by a toque
From the relationship dW = τ dθ, we obtain the expression of the power(
the rate at which work is done by the torque):
P = dW/dt = τ dθ/dt = τ ω
Power delivered by a toque :
P = τ ω
The work done by a torque and its power delivered may be
negative. This is the case when the torque is slowing the rotation :
the angle θ and the torque due to the force have opposite signs.
|
|