Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
| Rotation : Force & torque
1. Superman stops earth from spinning
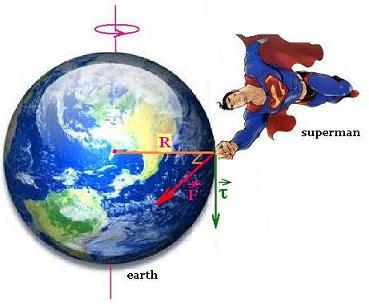
To stop the earth to rotate, Superman will exert a force F
somewhere at the equator. Since the earth rotates toward east,
Superman will fly in the opposite direction. For Example he
will fly from Somalia, cross the Atlantic ocean to land at
Ecuador that will constitute the application point of
the force F.
1. Exerting a torque
We have the following rotational Newton's second law:
Σ τext = τnet = Ie α
Where
Ie is the moment of inertia of the earth (solid sphere)
= (2/5)MR2
M the mass of the earth, R its radius, and α is its deceleration.
The toque τnet that will
decelerate the rotation of the earth is due to the torque
τf = R x F = R F of the superman.
Therefore
Ie α = τf = R F
The force that will be exerted has the magnitude:
F = Ie α/R = ((2/5)MR2) α/R =
(2/5) M R α
F = (2/5) M R α
(1)
1.1. The value of the deceleration
To stop the sphere to rotate, the angular speed will
decrease from ω to zero in Δt seconds.
Therefore
Δω = ω - 0 = ω
and
The deceleration α of the sphere is then:
α = Δω /Δt
We have:
ω = 2π/T,
where T is the period of revolution of the earth = 1 day
= 24 x 3600 = 86,400 seconds
Therefore
ω = 2π/86,400 seconds = 1.45 x 10-4 rad/s
with Δt = 14.5 seconds,
α = 1.45 x 10-4 /14.5 =
1.00 x 10-5 rad/s2
1.2. The magnitude of the force
R = 6.371 x 106 meters
M = 5.974 x 1024 kilograms
F = (2/5) 5.974 � 1024 6.371 x 106 1.00 x 10-5
=
(2/5) 5.974 6.371 x 1025
=
15.22 x 1025 Newtons.
F = 1.5 x 1026 Newtons.
2. Exerting a force
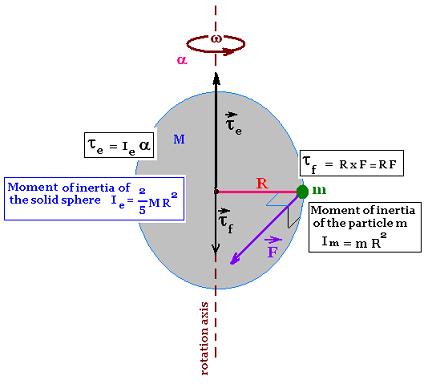
Since we have available the deceleration α, then
the tangential acceleration a = R α, we can apply
Newton's second law F = m a = m R α.
But what is the value of the mass m?
The value of the mass m can found by considering
the sphere equivalent to a particle of mass m fixed
at the end of a massless rod of length the earth's radius R.
A particle of mass m fixed
at the end of a massless rod of length R has a moment of inertia
equal to Im = m R2
The moment of inertia of the earth (solid sphere) is
Ie = (2/5)M R2
Equating the two moments of inertia gives:
Ie = Im (2)
or
(2/5)M R2 = m R2
That gives:
m = (2/5) M
m = (2/5) M
(3)
Hence
Exerting a tangential force F on the mass m =
(2/5) M , and applying Newton's second law
give:
F = m a = m R α = (2/5) M R α
That is the result found above in the relationship (1).
2. Superman stops earth from orbiting
2.1. Tangential speed of the earth
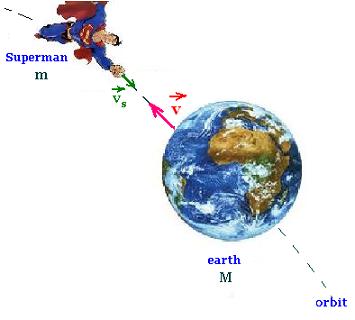
The orbit of the earth around the sun is an ellipse
of semi-major axis equal to 152 million kilometers,
and semi-minor axis equal to 147 million kilometers. Therefore,
the average radius is equal to d = (152 + 147)/2
= 150 million km
The circumference of this equivalent circle is
C = 2π d = 2 π (150,000,000 km)
= 940,000,000 km
The period of revolution T of the earth around the sun is one year.
That is
T = 365.25 days = 365.25 24 3600 seconds
= 31,600,000 s
Then the speed of the earth is
v = C/T = 940,000,000 km/31,600,000 s
= 30 km/s
The tangential speed of the earth is:
v = 30 km/s
2.2. The speed of Superman
To stop orbiting the earth, Superman's head on collision with the
earth must comply with conservation of the momentum law. That is
for the collision:
(M,v) + (m,vs),
M v - m vs = 0
Or
vs = M v/ m
v = 30 km/s
M = 5.974 x 1024 kilograms
m = 60 kg
vs = 5.974 x 1024 3 x 104/60
= 5.974 x 1027 3/6 =
3.0 x 1027 m/s !
vs = 3.0 x 1027 m/s !
Compared to the speed of light in the vacuum of 3.0 x 108 m/s
Three thousand trillions times faster than light !
|
|