Rotation
Contents
Applications
Worked examples
© The scientific sentence. 2010
Formulas
θ = (1/2) α t2 + ωot + θo
ω = α t + ωo
ω2 - ωo2 = 2 α (θ - θo)
ar = ω2(t) r
at = α r
Circ. Unif. motion:
1 rev = 2π rad
θ = ωt
v = ω r
T = 2π/ω = 1/ƒ
ar = ω2r = v2/r
at = 0
|
|
Torque
1. definition
We know that when we open or close a door, it requires more force
to open or close it if we pull or push close to the hinges. But
the farther we are from the hinges, the easier it becomes. The
same effect occurs if we use a wrench to loosen or tighten a bolt.
We introduce then the concerpt of torque that takes into
account a force and a distance (or radius)from
the center of rotation or the axis of rotation to
the point of application of this force. It is the torque
that tends to cause an object to rotate.
Linear acceleration of an object stems from
applying exterior force(s) to this object. Angular
acceleration is caused by applying a torque.
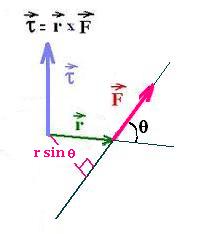 The expression of a torque is:
τ = r x F = r F sin θ
θ is the angle between r and F.
The expression of a torque is:
τ = r x F = r F sin θ
θ is the angle between r and F.
τ = r x F = r F sin θ
θ is the angle between r and F
r is the radius, that is the distance from the rotation
axis to the point of application of the force F. The force F
is the tangential force, hence the radius is called
the lever arm.
A torque is a vector, perpendicular to r and F. Its direction
is along the axis of rotation. By convention, the sign of a torque
is positive for a counter-clockwise rotation and negative for
clockwise rotation. The magnitude of τ is r F sin θ
θ is the angle between the vectors r and F. Its unit is the N.m.
We can recall also that if the line of action of a force passes
though the axis, the torque aboout that axis is zero
2. Example:
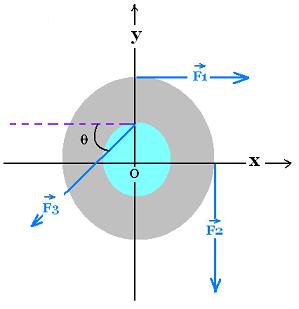 The wheel has two radii a = 10 cm and b = 20 cm.
The forces exerted on the edges have the following
magnitudes: F1 = 3 N, F2 = 4 N, and F3 = 15 N. The angle θ
is equal to 30o. What is the magnitude of the produced
net torque τ?
The components of the net force are:
Fx = F1 - F3 cos θ = 3 - 15x(31/2 /2) = - 9.99
Fy = F2 + F3 sin θ = 4 + 15/2 = 11.5
The magnitude of the resultant force is:
F = [Fx2 + Fy2]1/2 = 15.23 N
Its orientation is:
θ = tg - (11.5/-9.99) = - 49o
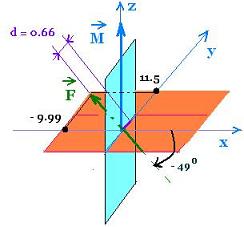
The clockwise equivalent torque has the magnitude of :
M = b F1 + b F2 - a F3 cosθ - 0 F3 sin θ = + 10.10 N.cm. It is
oriented along with the z-axis pointing towards us.
The force F = 15.23 N and the moment M 10.10 N.m can be reducted to
a single force at the distance d = M/F = 10.10/15.23 = 0.66 cm
The wheel has two radii a = 10 cm and b = 20 cm.
The forces exerted on the edges have the following
magnitudes: F1 = 3 N, F2 = 4 N, and F3 = 15 N. The angle θ
is equal to 30o. What is the magnitude of the produced
net torque τ?
The components of the net force are:
Fx = F1 - F3 cos θ = 3 - 15x(31/2 /2) = - 9.99
Fy = F2 + F3 sin θ = 4 + 15/2 = 11.5
The magnitude of the resultant force is:
F = [Fx2 + Fy2]1/2 = 15.23 N
Its orientation is:
θ = tg - (11.5/-9.99) = - 49o
The clockwise equivalent torque has the magnitude of :
M = b F1 + b F2 - a F3 cosθ - 0 F3 sin θ = + 10.10 N.cm. It is
oriented along with the z-axis pointing towards us.
The force F = 15.23 N and the moment M 10.10 N.m can be reducted to
a single force at the distance d = M/F = 10.10/15.23 = 0.66 cm
3. Static equilibrium
To be in static equilibrium, arigid body must be in both translational
equilibrium Σ Fext = 0 and rotational equilibrium.
The condition for the latter is written as a vector equation:
Σ Τext = 0,
where Σ Τext is the
sum of the torques produced by the external forces acting on the
rigid body. The rotational equilibrium balances the tendencies
to rotate clockwise and counterclocwise about any axis.
static equilibrium: vector equations
The net external force is zero: Σ Fext = 0
The net external torque is zero: Σ Τext = 0
34. Example
What are the values of the forces F2 and F3 in the example
above to set a static equilibrium ?
We have:
0 = F1 - F3 cos θ then: F3 = F1/cos θ
0 = F2 + F3 sin θ then : F3 = - F2/sin θ
0 = b F1 + b F2 - a F3 sin θ - 0 F3 cosθ
Then: F3 = (b F1 + b F2 )/a sinθ
F1/cos θ = - F2/sin θ or F2 = - F1 tan θ
Then: F2 = - 1.73 N
F3 = b(F1 + F2 )/a sinθ = b(F1 - F1 tan θ )/a sinθ =
b F1 (1 - tan θ )/a sinθ =
20 x 3 x ( 1 - 3/1/2/3)/10 x (1/2)
= 5.07 N
|
|