Rotation: exercises
Turntable - MP3
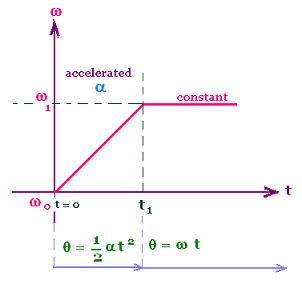
Consider a turntable of 30 cm of diameter starting with an angular speed ωo = 0 rad/s.
It takes t1 - to = t1 to get a
constant angular speed ω = ω1.
From the time t = 0 to the time t1, the
circular motion is accelerated, and from t1 the
motion is uniform.
Therefore
1. The acceleration
The acceleration of the system is :
α = Δω/Δt
= (ω1 - ω0)/(t1 - t0) =
(ω1 - 0)/(t1 - 0) = ω1/t1
α = ω1/t1
ω1 = 3333 revolutions/mn = 3333 rev/60 s = 55.55 rev/s
Since 1 rev = 2π radians, we get:
ω1 = 55.55 x 2π rad/s = 349.031 rad/s
ω1 = 349.031 rad/s
With t1 = 0.02 s
α = 349.031/0.02 rad/s2 = 17451.54 =
1.75 x 104 rad/s2
α = 1.75 x 104 rad/s2
2. The number of revolutions while
the system is accelerated
θ = (1/2) α t2 + ωo t + θo
= (1/2) α t2 + 0 + 0 = (1/2) α t2
θ = (1/2) α t2
The number of revolutions from to = 0 to the time t1 is :
θ = (1/2) α t12 =
(1/2) (1.75 x 104 rad/s2) (0.02 s)2 =
3.490 rad = 3.490 rad /2π rev = 0.5555 rev
At t = 0.02 s, the turntable has rotated 0.5555 rev.
At t = 0.02 s, the MP3 has
rotated 0.5555 revolutions.
From t = t1 = 0.02, the motion is uniform, so:
ω = ω1 = constant
= 3333 revolutions/mn = 349.031 rad/s, and
θ = ω1 t
θ = ω1 t
3. The number of revolutions during 0.05 seconds
At the time t = 0.05 = 0.02 + 0.03 seconds, we have:
0.5555 rev (in 0.02 sec) + θ rev (in 0.03 s) =
We have:
θ rev (in 0.03 s) =
ω1 0.03 s = (349.031 rad/s) (0.03 s) =
10.471 rad = 10.471/2π rev =
1.666 rev.
As it has already done 0.5555 rev (from t = 0 to t = t1) , the
number of revolutions done is 0.5555 + 1.666 = 2.222 revolutions.
Number of revolutions during 0.05
seconds = 2.222 revolutions.
4. The required time to make two revolutions
Two revolutions is greater than 0.5555 revoltion, so the
related time is greater than t1 = 0.02 s. We apply
the formula θ = ω1 t
2 - 0.5555 = θ = ω1 t, so
t = (2 - 0.5555) 2π /(349.031 rad/s) = 0.026 s
t is the time to make 2 - 0.5555 = 1.4445 rev from
t = t1 = 0.02 s. Therefore
The total time is 0.02 + 0.026 = 0.046 s.
Required time to make two
revolutions = 0.046 s.
5. The magnitude of the radial and the
tangential acceleration
1. If t < t1 = 0.02 s: the circular motion is accelerated
ar = ω2(t) r
at = α r
At the time t , ω(t) = α t
With t = 0.01 s (< t1 = 0.02 s), we have:
ω(t) = α t = (1.75 x 104 rad/s2) (0.01 s) =
(1.75 x 102 rad/s
Thus:
ar = ω2(t) r =
(1.75 x 102 rad/s2(t) (0.30 /2 m ) =
4593.75 m/s2
at = α r = (1.75 x 104 rad/s2 ) (0.30 /2 m ) =
2625 m/s2
ar = 4593.75 m/s2
at = 2625 m/s2
2. If t > t1 = 0.02 s: the circular motion is uniform
ar = ω12 r = (349.031 rad/s) 2 (0.30 /2 m )
=
18273.396 m/s2
at = 0 (because the motion is uniform from the time t= t1)
ar = 18273.396 m/s2
at = 0
|