Rotation Kinematics: Bicycle

1. presentation

The interesting parts, in Kinematics point of view, on a bicycle are:
- The rear nad the front wheel (tires),
- The rear gear that is a sprocket,
- The front gear that is a chainring,
- The chain connecting the front gear to the back gear,
- The pedal that provides an engine torque.

While pedaling, the front gears rotates at the same angular speed as the two petals, while the back gears rotates at the same angular speed as the wheel.

The chain that connect the two gears has the same linear velocity at every point on the chain, especially, on both the front and the back gears.

2. Relationship between pedal
and wheel angular speeds

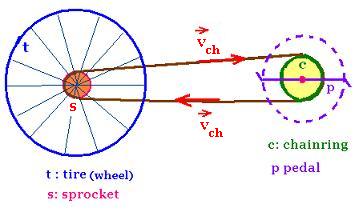
R_p = radius of the pedal
ω_p = angular speed of the pedal
v_p = tangential speed of the pedal
v_p = ω_p R_p    (1)

R_c = radius of the chainring ω_c = angular speed of the chainring = angular speed of the pedal
ω_p = ω_c    (2)
v_c = tangential speed of the chainring = speed of the chain v_ch
v_c = v_ch
   (3)
v_ch = ω_c R_c    (4)

R_s = radius of the sprocket
ω_s = angular speed of the sprocket
v_s = tangential speed of the sprocket = speed of the chain = tangential speed of the chainring
v_s = v_c = v_ch    (5)
v_s = v_ch = ω_s R_s    (6)

R_t = radius of the tire (wheel)
ω_t = angular speed of the tire = angular speed of the sprocket
ω_s = ω_t    (7)
v_t = tangential speed of the tire
v_t = ω_t R_t    (8)

Therefore, the last formula (8):
v_t = ω_t R_t

Using (7) becomes:
v_t = ω_s R_t

Using (6) and (5)
v_t = (v_ch/R_s) R_t

Using (4) and(3):
v_t = (ω_c R_c/R_s) R_t

Using (2):
v_t = (ω_p R_c/R_s) R_t

Finally, using (1):
v_t = (v_p R_c/R_p R_s) R_t

v_t = = v_p (R_c/R_p R_s) R_t

Using (10 and (8):

When we change the gears on the bike, we change the ratio R_c/R_s in effect.

For a fixed pedaling angular speed ω_p; changing to a smaller gear R_c in the front, or a larger one R_s in back, provides a smaller angular speed ω_t for the wheel.
To go faster, invert the changing in the gears: greater R_c and smaller R_s.
To move anyway, we have to pedal.

3. Example

With the following data:
r_t = 50 cm
r_s = 10 cm
r_c = 14 cm
r_p = 20 cm ,
we have :
v_t = 3.50 v_p

If the bicycle rolls a distance d during a period of time t at a constant speed; the displacement of the center of mass CM, which is the center of the wheel, is d = v_cm t, and its acceleration is zero.

For each revolution of the wheel, having a circunference C = 2πr_t, the CM has translated, that is moved on a straight line, a distance d₁ = 2πr_t.
This distance d₁ lasts the period T of the revolution of the wheel. r_t is the radius of the wheel, ω_t is its angular speed, and v_t its tangential speed. Therefore:
d₁ = 2πr_t = v_cm T

Since: 2π/T = ω_t, we get:
v_cm = 2πr_t/T = ω_t r_t

Since the tangential speed of the wheel is v_t = ω_t r_t, we get then:
v_cm = v_t = ω_t r_t

Now, d₁ becomes:
d₁ = v_cm T = ω_t r_t T,
and
d = v_cm t = ω_t r_t t
or
ω_t = d/r_t t

With the following data:
d = 4 km = 4000 m, and t = 30 mn = 1800 s, r_t = 50 cm,

we have:
ω_t = 4000/(0.5 1800) = 4.44 rad/s
Since 1 revolution = 2π rad , we have
ω_t = 4.44 / 2π = 0.71 rev/s

Along the path d, the wheel has rotated (0.71 rev/s) 30 mn = 0.71 1800 rev = 1273.24 revolutions.