Statics
Contents
Applications
© The scientific sentence. 2010
|
Static Equilibrium
1. Definition
For Static system, to be at equilibrium, The net force
and the total moment of a system are zero.
ΣF = Fnet = 0
Σ M(F)/any-axis = 0
The total moment is defined as:
Σ M(F)/axis = Σ Mx(F)/axis i +
Σ My(F)/axis j + Σ Mz(F)/axis k
Therefore:
Σ Mx(F)/axis = 0
Σ My(F)/axis = 0
Σ Mz(F)/axis = 0
The following relationships are true:
ΣF = Fnet = 0
Fnet = Fnet-x + Fnet-y = 0
Fnet-x = ΣF (over x) = 0
Fnet-y = ΣF (over y) = 0
M(Fnet)(about z) = 0
M(Fnet-x)(about z) + M(Fnet-y)(about z) = 0
Σ M(F)(over x)(about z) = 0
Σ M(F)(over y)(about z) = 0
2. Example
Two forces F1 and F2 are exerted on the rod at the distance
d1 and d2 from the fulcrum respectively.
We have the following formula:
ΣF = Fnet = F1 + F2 = 0
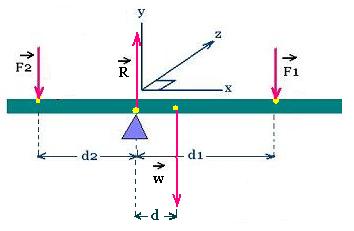
The rod is at equilibrium on a fulcrum. Its mass
is of 0.5 kg, d = 20 cm, d1 = 30 cm.
Where to exert a force F2 to have
F1 = F2 = 10.0 N, and stay at equilibrium?
Fnet-x = ΣF (over x) =
0 + 0 + 0 + 0 = 0
Fnet-y = ΣF (over y) = 0
- F2 - W - F1 + R = 0
Then
R = F2 + W + F1
With F2 = 2F1, we have
R = W + 2F1
= 0.5 9.8 + 2 10.0 = 24.9 N
R= 24.9 N
Σ M(F)(z-axis-fulcrum) = 0
M(- F2) + M(- W) + M(- F1) + M(R) = 0
d2 F2 - d W - d1 F1 + 0 = 0
Then:
d2 F2 - d1 F1 = d W
With F2 = 2 F1, we have:
2 F1 d2 = d W + F1 d1
d2 = (d W / 2F1)+ d1/2
d2 = (d W /2 F1) + d1/2
0.20 0.5 9.8 / 2 10.0) + 0.30/2 = 0.20
d2 = 20 cm
d2 = 20 cm
|
|