Statics

Lid of a roof scuttle

Steps to follows:
- Understand the mechanism,
- Draw all the forces
- Draw the FBD,
- Use ∑ F = 0 and ∑ M(F)_any-point = 0.



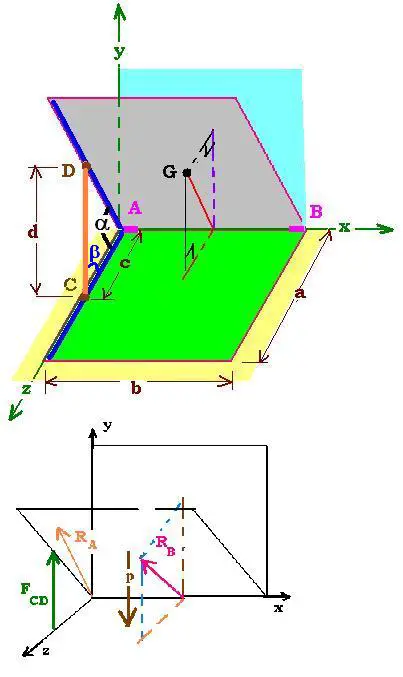
We have three forces:
A) The force exerted by the rod CD: F_CD.
B) The reactions at the hinges A and B:
- Recation on A: R_A, and
- Reaction on B: R_B, and


Since the hinge at B does not exert any axial thrust, R_B,x (component over x) is zero.

We have:
R_A = R_A,x i + R_A,y j + R_A,z k
And
R_B = R_B,y i + R_B,z j

∑ F = 0
R_A + R_B + F_CD + P = 0

Over x:
∑ F_x = 0
= R_A,x + R_B,x + F_CD,x + P_x = 0
0 + 0 + 0 + 0 = 0

Over y:
∑ F_y = 0
= R_A,y + R_B,y + F_CD,y + P_y
= R_A,y + R_B,y + F_CD,y - P


Over z:
∑ F_z = 0
= R_A,z + R_B,z + F_CD,z + P_z
= R_A,z + R_B,z + F_CD,z + 0

∑ M[F]/A = 0
M[R_A]/A + M[R_B]/A + M[F_CD]/A + M[P]/A = 0

M[R_A]/A = 0

M[R_B]/A = (b,0,0) x(0, R_B,y, R_B,z) =
(0,- b R_B,z, b R_B,y)

M[F_CD]/A = (0,AD sin α,AD cos α) x (0, F_CD,y , F_CD,z) =
(AD sin α F_CD,z - AD cos α F_CD,y,0,0 )

M[P]/A = AG x P = (b/2,(a/2)sin α ,(a/2)cos α ) x (0, - P, 0) =
(1/2) (P a cos α ,0, - P b)
∑ M[F]/A = 0
= 0 +
(0, - b R_B,z, b R_B,y) +
(AD sin α F_CD,z - AD cos α F_CD,y, 0,0 ) +
(1/2) (P a cos α , 0, - P b)

Then:
AD sin α F_CD,z - AD cos α F_CD,y + (1/2) P a cos α =
0 - b R_B,z = 0 → R_B,z = 0

R_B,z = 0

b R_B,y - (1/2) P b = 0 → R_B,y = P/2

R_B,y = P/2

Over y:
R_A,y + F_CD,y = P/2

Over z:
R_A,z + F_CD,z = 0

AD sin α F_CD,z - AD cos α F_CD,y + (1/2) P a cos α = 0

F_CD,z = - F_CD cos β
F_CD,y = + F_CD sin β

AD sin α (- F_CD cos β) - AD cos α (+ F_CD sin β) + (1/2) P a cos α = 0

AD F_CD [- sin α cos β - cos α sin β] + (1/2) P a cos α = 0

AD F_CD [sin α cos β + cos α sin β] = (1/2) P a cos α

AD F_CD sin (α + β) = (1/2) P a cos α
Thus:
F_CD = P a cos α /2 AD sin (α + β)

F_CD = P a cos α /2 AD sin (α + β)

And:
R_A,z = - F_CD,z = F_CD cos β
= P a cos α cos β /2 AD sin (α + β)

R_A,z = P a cos α cos β /2 AD sin (α + β)

and:

F_CD,y = + F_CD sin β =
P a cos α sin β /2 AD sin (α + β)

R_A,y + F_CD,y = P/2
R_A,y = P/2 - F_CD,y =
P/2 - P a cos α sin β /2 AD sin (α + β)

R_A,y = P/2 - P a cos α sin β /2 AD sin (α + β)

To find AD and the angle β, we can use the sine law:
d/sinα = c/sin(α + &β) = AD/sin β
Then:
sin(α + β) = c sinα/d α + β = arcsin [c sinα/d]
Thus:
β = arcsin [c sinα/d] - α

β = arcsin [c sinα/d] - α
And
AD = d sinβ /sin α = d sin{arcsin [c sinα/d] - α} /sin α

AD = d sinβ /sin α =
d sin{arcsin [c sinα/d] - α} /sin α