Statics
Contents
Applications
© The scientific sentence. 2010
|
Static equilibrium & muscles
In this application, we will apply again the two static equilibrium
formulas, and realize that the forces in muscles can be extremely large.
1. The triceps muscle:
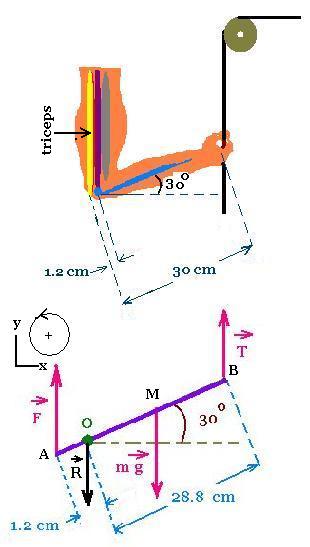
1.1 The forces acting on the forearm:
1. A forearm pulls downward a rope with a force of 50 N. According to Newton's third law,
the rope exerts a force upward (tension) T of 50 N on the forearm.
This tension in the rope acts at a distance
OB = 30 - 1.2 = 28.8 cm from the pivot.
2. The weight of the forearm considered as a rod of length 30 cm is
mg = 2 x 9.81 = 19.62 N.
This weight acts downward at the centre of mass, that
is at the lever arm equal to OM = 30/2 cm - 1.2 cm = 13.8 cm from the pivot.
3. The force F is exerted by the triceps muscle that pulls on the forearm
upward.
This force acts at a distance OA = 1.2 cm from the pivot.
4. The reaction R of the the bones in the upper arm on the
forearm. It is the downward force at the joint O.
1.2 The forearm in static equilibrium:
The related torques for each force are:
τ (T) = + T OB cos 30
τ (mg) = - mg OM cos 30
τ (R) = 0
τ (F) = - F OA cos 30
The system "forearm" is in static equilibrium, that is
the net force is zero and the net torque is zero.
Translational equilibrium:
Σ F = 0
Rotational equilibrium
τnet = Σ τext = 0
1. To determine F, we apply
τnet = 0:
T OB cos 30 - mg OM cos 30 - F OA cos 30 = 0
Or
T OB - mg OM - F OA = 0
Hence
F = (T OB - mg OM)/ OA
(50 x 28.8 - 2 x 9.8 x 13.8)/ 1.2 =
975 N
F = 975 N
Remark that the angle of inclination θ = 30o is
irrelevant. That could be any angle including the horizontal.
2. To determine R, we apply
Σ (forces) = 0:
Along the y-axis, we have:
+ T - mg - R + F = 0
Then:
R = T + F - mg =
50 + 975 - 2 x 9.8 = 1005.38 N
R = 1005 N
2. The biceps muscle:
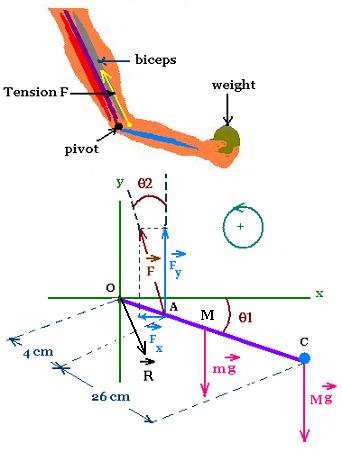
We need to know the biceps tension F required
to Lift a weight.
We choose as a free body the forearm . Therefore
the acting forces are drawn in its related
free body diagram.
The acting forces are:
1. The weight is Mg, M = 5 kg.
This weight has a lever arm OC cos θ1; with
OC = 30 cm.
Its torque related to the pivot is :
τ(weight) = - M g OC cos θ1
2. The forearm makes an angle
θ1 with the horizontal equal to 30o.
It has a mass of 2 kg. Its weight
acts on the center of mass.
The corresponding
lever arm is OM cos θ1 with OM = OC/2 = 15 cm.
Its torque related to the pivot is:
τ(forearm) = - m g (OC/2) cos θ1
3. The tension of the muscle in the biceps is F.
It has a lever arm OA cos θ1 from the pivot with OA = 4 cm.
The tension F is projected into its two components:
Fx along the x-axis and Fy along the y-axis.
1.
The lever arm of Fx is OA sin θ1 .
Fx = F sin θ2
Its torque related to the pivot is :
τ(Fx) = - Fx OA sin θ1 =
- F sinθ2 OA sin θ1
2.
The moment arm of Fy is OA cos θ1.
Fy = F cos θ2
Its torque related to the pivot is:
τ(Fy) = + Fy OA cos θ1 =
+ F cos θ2 OA cos θ1
4. The reaction R at the pivot O produces no
torque because the pivot is chosen as
the rotation axis.
The reaction R is inclined because its x-component
must balance the x-component of the tension F.
Its y-component must be directed downward to balance,
about the point A, the negative torque produced by the
weight en C and the weight of the forearm on M. Therefore
R must produce an opposing positive torque about the point A.
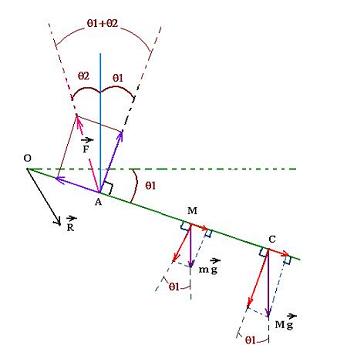
Applying the rotational equilibrium: Στ = 0, for
the system "forearm", yields:
τ(weight) + τ(forearm) + τ(F)
+ τ(R) = 0
with
τ(F) = τ(Fx) + τ(Fy)
Therefore
- M g OC cos θ1 - m g (OC/2) cos θ1
- F sinθ2 OA sin θ1 + F cos θ2 OA cos θ1
+ 0 = 0
Rearranging gives:
M g OC cos θ1 + m g (OC/2) cos θ1 =
F OA (cos θ2 cos θ1 - sinθ2 sin θ1)
Using the trigonometric formula:
cos(a + b) = cos a cos b - sin a sin b, gives:
cos θ2 cos θ1 - sinθ2 sin θ1
= cos( θ1 + θ2)
Hence:
M g OC cos θ1 + m g (OC/2) cos θ1 =
F OA cos( θ1 + θ2)
Therefore:
F = g OC cos θ1 (M + m/2) /
OA cos( θ1 + θ2)
F = 9.8 x 30 cos (30) x (5 + 2/2)/ 4 x cos (30 + 5)
= 466.23 N
F = 466.23 N
We can find the above result quickly just by
projecting all the three forces over the line OC
of the forearm, and have:
OA F cos (θ1 + θ2) - mg (OC/2) cos θ1 - Mg OC cos θ2 = 0
and find as above:
F = g OC (M + m/2) cos θ1 / OA cos(θ1 + θ2)
3. The tension force in the Achilles tendon:
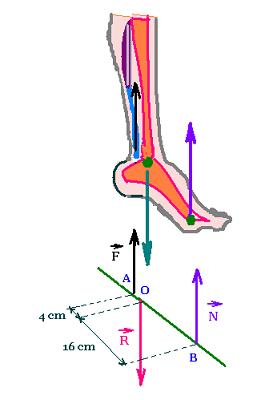
A foot of a person of 60 kg standing on the ball of one foot.
Each foot undergoes a normal N = 60 x 9.8 /2 N. Three
forces act on the foot to maintain this equilibrium:
1. The normal force N,
2. The contact or reaction force R at the ankle joint, and
3. The tension force F in the Achilles tendon.
We want to find the magnitude of (a) the tension F in the
Achilles tendon and the reaction force at the
ankle joint.
At the point O:
Σ τ = 0
That gives:
OA F = OB N
Therefore:
F = (OB/OA) N = (16/4) 60 x 9.8/2 = 1176 N
F = 1176 N
The translational equilibrium is written as:
Σ F = 0
That gives:
N - R + F = 0
Therefore:
R = N + F = + 30 + 1176 = 1206 N
R = 1206 N
|
|