Statics
1. Sign hooked on a boom
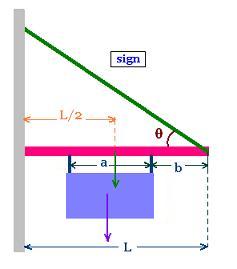
Let's consider a sign of length a hooked on a boom at a
distance b from the left.
2. The forces on the whole system
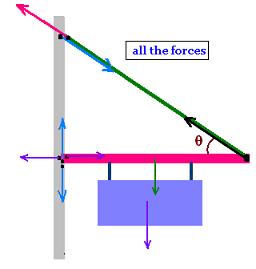
The forces on the whole system are:
1. The action of the wire on the boom and its reaction
2. The weights of the sign and the weight of the boom.
The
point of application of the sign's weight is at the distance:
x = L - a - b + a/2 = L - b - a/2. The point of application of the
boom's weight is at the distance: L/2.
3. The action of the boom on the wall and its reaction
4. The action of the wire on the wall and its reaction
3. Free body diagram for the
system "boom+sign":
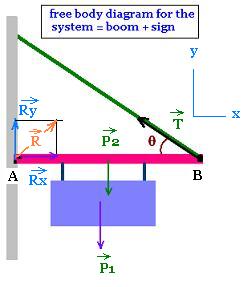
The free body diagram of the system boom+sign shows
only the force on this single system:
1. The action of the wire on the boom
2. The weights of the sign and the weight of the boom.
3. The reaction of the wall on the boom
4. Values of the tension and the
reaction of
the wall:
The static equilibrium is:
Σ F = R + P1 + P2 + T = 0 (1) , and
τ = Σ M (F) = M(R) + M(P1) + M(P2) + M(T) = 0 (2)
Over x-axis:
(1): Rx + 0 + 0 - T cos θ = 0 , that is:
Rx = T cos θ (3)
Over y-axis:
(1): Ry - P1 - P2 + T sin θ = 0 , that is:
Ry = P1 + P2 - T sin θ (4)
Over x-axis and about the point A:
(2): M(Rx) + M(P1x) + M(P2x) + M(Tx) = 0
0 + 0 + 0 + 0 = 0
Over y-axis and about the point A:
(2): M(Ry) + M(P1y) + M(P2y) + M(Ty) = 0
0 - P1 x - P2 L/2 + T sin θ L = 0
That is:
T sin θ L = P1 x + P2 L/2 =
= g m1 (L - b - a/2) + m2 g L/2
T = g [m1 (L - b - a/2) + m2 L/2]/(sin θ L)
Using (3):
Rx = T cos θ = g cos θ[m1 (L - b - a/2) + m2 L/2]/(sin θ L)
Using (4):
Ry = P1 + P2 - T sin θ = g(m1 + m2) - g [m1 (L - b - a/2) + m2 L/2]/L
Using Pythagoras' theorem, we get:
R = [Rx2 + Ry2]1/2
T = g [m1 (L - b - a/2) + m2 L/2]/(sin θ L)
Rx = g cos θ[m1 (L - b - a/2) + m2 L/2]/(sin θ L)
Ry = g(m1 + m2) - g [m1 (L - b - a/2) + m2 L/2]/L
|