Physics :
Statics
Cable or bridge.

1. The forces acting on the system

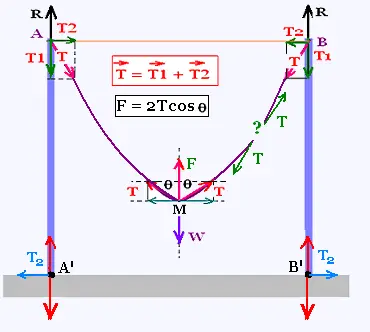
The system is composed of the two poles and the cable. In the simple case, we consider the weight "W" of the cable acts on the middle of this cable as in the point M. The system is in equilibrium. The forces acting on the system are shown at each point by a free body diagram:

T = T1 + T2
T1 + R = 0 (on A and B)

On M, horizontally: T sin θ - T sin θ = 0,
On M, vertically: T cos θ + T cos θ = W, or
2 T cos θ = W

We are particularly interested to find the expression of the tension T along with the cable strung, where its weight is distributed uniformly along with its length.

2. The differential equation:

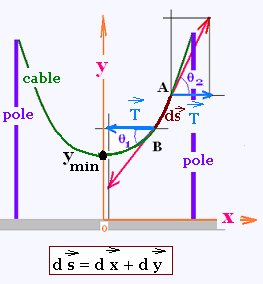
A cable is hanged freely between two supports. It has a uniform weight w per unit length (in Newtons/meter).

We are to derive a second-order differential equation, that gives the equation of the curve formed by the cable.

Any arc "ds" taken in the cable is in equilibrium due to the related tensions at the extremities of the arc. The projection of these two tensions are:

• Along x axis: T + T = 0
(vectorially, the sum of the two horizontal components cancel),
• Along y axis: The difference of the vertical components of the extreme tensions is equal the total weight on the arc; that is: >

T tgθ2 - T tgθ1 = w ds     (1)

Vectorially, we have ds = dx + dy, so

ds² = dx² + dy²     (2)

At a certain point such as A, tg θ is the slope of the curve, that is:

tg θ = dy/dx    (3)

Thus:

tgθ2 dy2/dx, and tgθ1 = dy1/dx. Then:

tgθ2 - tgθ1 = Δ (tg θ)     (4)

As the angles are small, we can write:

Δ (tg θ) = d (tg θ)

Using the relationship (3), (4) becomes:
Δ tg θ = tgθ2 - tgθ1 = d(tg θ) = d(dy/dx)

Using the relationship (2), (1) becomes:
T d(dy/dx) = w [dx² + dy²]^1/2

The differential of the two sides yields:
T (d²y/dx²) = w [dx² + dy²]^1/2 /dx =
w [1 + (dy/dx)²]^1/2

We find the differetial equation:

d²y/dx² = (w/T)[1 + (dy/dx)²]^1/2     (5)

3. The solution of the equation:

Now, what is the solution of this equation?
We will use:

• Hyperbolic sine:
sinh x = (e^x - e^-x)/2,

• Hyperbolic cosine:
cosh x = (e^x + e^-x)/2,

• The relationship between them:
cosh²x - sinh²x = 1, and

• The related derivatives:
. d(sinhx)/dx = cosh x
. d(cosh x)/dx = sinh x

Let then:

dy/dx = sinh z , then:
d²y/dx² = cosh z dz/dx
= [1 + sinh z²]^1/2 dz/dx = [1 + (dy/dx)²]^1/2 dz/dx .

According to the relationship (5), we have then:
cosh z dz/dx = (w/T) [1 + sinh z²]^1/2 = (w/T) cosh z

Therefore:

cosh z dz/dx = (w/T) cosh z , so dz/dx = (w/T).
The integrle gives: z = (w/T) x + K , where K is a constant.

Then: dy/dx = sinh z = sinh [w/T) x + K] = (1/2) [exp {w/T) x + K} - exp {- ((w/T) x + K)}]


Now, we determine the constant K.

dy/dx is the derivative of "y" with respect to "x". It is equal to zero at the minimum x = 0 , which gives y_min for the value of "y". Hence:

dy/dx (at x = 0 ) = 0 , that leads to (1/2) [exp {K} - exp {- K}] = 0 or K = 0.

Therefore:

dy/dx = sinh z = (1/2) [exp {(w/T) x } - exp {- (w/T) x }] = sinh [(w/T) x]

Integrating :

y = ∫ sinh [(w/T) x] dx = (T/w) ∫ sinh [(w/T) x] d((w/T)x) =
(T/w) cosh [(w/T) x] + C , where C is a constant.

We have: for x = 0 y = y_min, then:
y_min = (T/w) cosh [(0] + C = (T/w) + C , then : C = y_min - (T/w)

Therefore:

y = (T/w) cosh [(w/T) x] + y_min - (T/w)

The solution for the differential equation of the cable is:

y = (T/w) cosh (w x/T) + y_min - (T/w)