Statics
Contents
Applications
© The scientific sentence. 2010
|
Physics :
Statics
Leading a portable ladder
Leading a portable ladder
Abstract
We are often too busy to take into account some
details that are sometimes very important. When
we want to fix something set on the wall very high
from the floor, we use very often a ladder. We know by
practicing where to set approximately the the top of
a ladder in order to prevent sliding and falling when we stand it.
Knowing a little basic geometry and some knowledge of
Physics could give us some tips to know exactly what to
do in order to stay safe while working mounting a ladder.
In this article, we will understand one important precaution
to apply, derived from some Physics' laws, in order to
prevent falling.
Introduction
We will use, in this article, some basic notions of Physics;
mainly the two conditions for equilibrium which are the static
Newton's first law and the zero net torque for the system. The
first states the translational equilibrium and the second the
rotational equilibrium.
Using Mathematics, the first statement is written as Σ F = 0
and the second as Στ(F) = 0. F stands for forces and τ
for torques. Solving the related equations will be straightforward.
We will search for the expression of N(reaction of the wall on the
ladder); then the expression of the friction force; and comparing
them to derive the condition for that the ladder does not slip.
The result will give an important condition to know even if It
seems obvious. At least, It will be understood that Physics is
for something!
The problem:
Where would set the base of the ladder in
order to stay safe while working from it?
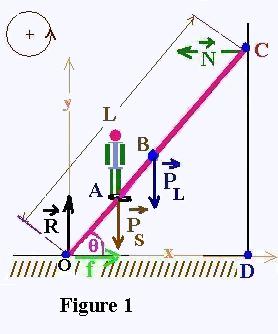
Free-body diagram for
all of the forces:
L is the length of the portable ladder.
OA = L/4
OB = L/2
OC = L
OD = Floor
DC = Wall
The forces in this system are:
• N : the reaction of the wall on the ladder.
This force is horizontal because the wall is
frictionless.
• f : is the friction force of the ladder on
the floor.
• R : the vertical component of the reaction
of the floor on the ladder. Note that the
real reaction of the ground on the ladder
is the sum of f and R.
• PS : the weight of John = g MS
• PL : the weight of the ladder = g ML
• g is acceleration gravity.
The solution:
John is stood up on the ladder at a point
X.(OX = L/n). n is any integer from 0 to 1; L/n
is the ladder's working length.
The first condition for equilibrium (the force balance equation)
for the system (John and the ladder) is:
Σ F = 0. That is:
• Over Ox: f = N (1)
• Over Oy: R = PS + PL (2)
This law does not suffice to get the expression of
the reaction N that we are searching for. We need the use
of the torque balance equation (the net torque about any axis in null).
That is :
Στ(Forces/axis) = 0. (the chosen axis is set on the floor,
perpendicular to R and f).
Σ τ(R) + τ(f) + τ(PS) + τ(PL) + τ(N) = 0 (3)
= 0 + 0 - (L/n)cosθ PS - (L/2)cosθ PL + Lsinθ N = 0
That is:
+ (L/n)cosθ PS + (L/2)cosθ PL = L sinθ N (4)
Thus:
N = g cosθ[(1/n) MS + (1/2) ML ] /sinθ
N =
g cotgθ[(1/n) MS + (1/2) ML] (5)
cotg θ = 1/tgθ = cosθ (6)
Not down that the friction issue does not depend
on the length of the ladder at all.
We know the the friction force can be written as:
f = μstatic
R = μstatic g (MS + ML) (7)
μstatic is the coefficient of static friction.
Physics behind Mathematics
What's the purpose?
John wants to mount the latter safely while working on it.
To have so, we must have friction abound the base of
the ladder. No friction means that the ladder will slide and
John will fall and likely be injured. That's not very pleasant!
Anyway, without friction on the base of the ladder, we can't even
set the ladder oblique; and it must stay vertical absolutely!
f = 0, yields:
cotgθ = 0 , thus cosθ = 0 , θ = π/2 = 90o. (8)
We need friction in the system. Friction governs the stability
of the ladder. But, even with friction, the fact that the ladder slides
(then moves) means that we have lost the equilibrium for the system. The issue
is then shifted to a dynamics problem. In this case, the second Newton's law tell
us Σ F = N - f = M a (M is the mass of the system which
is MS + ML; and
a is its acceleration. The system slides over the horizontal axis). Note that in these
circumstances, f = μkineticMg. To maintain the ladder stable, that is the system at rest,
the friction force f must be greater than N (f > N)
Comparing the two relationships (5) and (7) yields:
• The threshold ( When the ladder is on the verge of slipping) is given by:
μstatic g (MS + ML)
= g cotgθ[(MS/n) + (ML/2)] (9)
• The condition for the ladder to not slide is:
μstatic g (MS + ML)
> g cotgθ[(MS/n) + (ML/2)] (10)
Rearranging, we find:
μstatic (MS + ML)
> cotgθ[(MS/n) + (ML/2)]
Wood as well as steel have a weak coefficient of friction, but they remain
heavy material. Aluminum is often used as a substance to make ladders.
A ladder, generally weights about 50 N (mass of 5 kg). John weights about 800 N
(mass of 160 lbs = 80 kg). It is a good approximation to disregard ML
regarding MS.
( Of course, this approximation is not valid for a child of mass about ML!)
The inequality above becomes:
μstatic > (cotgθ)/n (11)
That is :
cotg θ < n μstatic
Using the expression of cotgθ It follows that:
Floor / Wall < n μstatic
(Recall Floor = OD and Wall = DC) (12)
The coefficient of static friction is always less than 1. Thus:
Floor / Wall < n .

n is the the ratio of the length of the ladder and the
ladder's standing length. Note that this result is an
extreme limit.
Conclusion
1. To be safe at the middle of the ladder (n = 2), extend the
base of the ladder at the most the double of the length of
the wall on the ground.
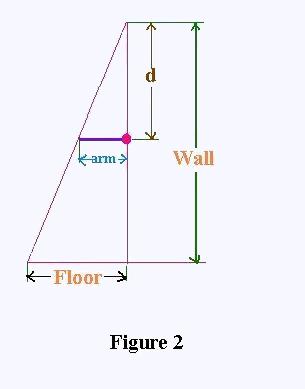
2. When we are working on a ladder, the reality is that we are
limited by the length of our arm which measures about 24 feet
(60 cm). To fix something set at the distance d from the top
of the ladder. This limitation; using similar triangles
(See figure 2) gives:
arm / d = Floor / Wall (13)
Which is the extreme limit.
Of course we must have:
arm / d < Floor / Wall
The distance d is generally greater than the width of the arm; thus
Floor / Wall < 1
That is Floor < Wall, which is a situation without any danger.
|
|