Nuclear Physics
The nucleus
Radioactivity
Applications
Particle accelerators
© The scientific sentence. 2010
|
Nuclear Physics &
Particle Physics
Particle accelerators
Cyclotrons
Cyclotrons
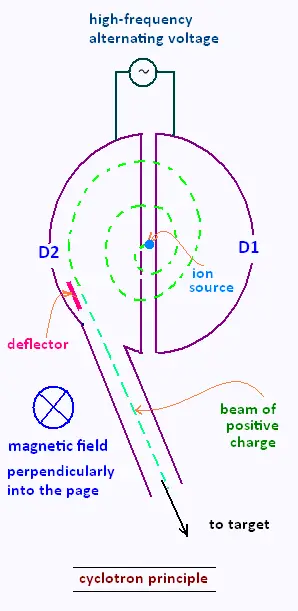
The length limitation can be overcome by making the charged particles follow a
circular path. In a cyclotron, charged particles are accelerated across
the gap between two 'D' shaped electrodes.
Meanwhile a perpendicular magnetic field moves the particles in a circle.
The radius of the circle increases after each successive acceleration, so the
path spirals out from the source at the centre to the target on the outside.
We will now derive the unique frequency ƒ at which the accelerating
voltage must alternate if the polarity of the D's is to reverse each
time the charged particle reaches the gap.
The force on the charge q moving at velocity v perpendicular to magnetic
field of strength B is:
F = Bqv
This provides the centripetal force necessary for circular motion:
F = mv2/r
m is the mass of the moving particle.
With v = ω r and ω = 2 π/T = 2 π ƒ , where
ω is the particle's angular velocity, T is the
orbiting period, and ƒ is the related frequency; we have:

F = Bqv = mv2/r or
Bq = mv/r = m ω =
2 m π ƒ
The frequency is therefore:
ƒ = Bq/ 2πm
Synchrotrons
The relatively small size of cyclotrons makes them useful
for producing energetic particles for medical treatments and testing
advanced industrial materials.
As the speed of the particles approaches that of light, however, the relativistic
mass increase becomes significant and this results in the charges arriving too late to
be accelerated across the gap. This puts a limit of about 1 GeV on the energy achievable.
Synchrotrons overcome this problem: the frequency of the alternating
voltage increases to match the flight time of the particles.
In a synchrotron, an increasing magnetic field confines a beam of accelerated
charged particles to an orbit of fixed radius. Synchrotrons are very large and
very expensive machines but they are capable of much higher energies
than cyclotrons.
Medical use of a cyclotron
A cyclotron is a machine used to make short-lived radioactive
isotopes that can be used for medical imaging or research.
A cyclotron does this by accelerating particles (such as hydrogen atoms) to
very high speeds and focusing them on a target substance where a reaction
takes place that produces a radioactive element.
Both the accelerated particles and target substance are specifically chosen to produce
the desired radioactive element.
Example:
The isotope Fluorine-18 (F-18) is produced in a cyclotron.
It is used in the tracer Fluorodeoxyglucose (FDG) which maps glucose
metabolism in the body.
Are also produced other radioactive isotopes such as Carbon-11 (C-11),
Gallium-68 (Ga-68), and Technetium-99m (Tc-99m) for medical imaging studies.
|
|