Nuclear Physics
The nucleus
Radioactivity
Applications
Particle accelerators
© The scientific sentence. 2010
|
α-decay and dose absorbed
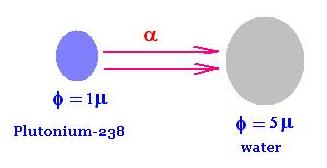
We are interested in evaluating the absorbed dose
of the α-decays projectile particles emitted from
a Plutonium-238, by a sample of water.
1. Plutonium element
Let's consider the Plutonium element:
Symbol: Pu
Atomic Number: 94
Number of Protons/Electrons: 94
Number of Neutrons: 150
Atomic Mass: (244.0) amu
Classification: Rare Earth (actinide series: synthetic or man-made).
Density at 293 K (200): 19.84 g/cm3 =
19.84 x 10-3 kg/10-6 m3 =
19.84 x 103 kg/m3
Isoptopes:
-- Plutonium-244, the most stable, of half-life
of about 80 million years.
-- Plutonium-240, with a high rate of spontaneous fission.
-- Plutonium-239, the most useful for nuclear weapons,
fissile as Plutonium-241 .
-- Plutonium-238 has a half-life of 88 years and emits
alpha particles. It is e heat source in thermoelectric generators.
We will focus on the istope 238.
2. Moles and Avogadro number
Avogadro number = 6.023 x 1023
1 uma = 12 x 10- 3 /12 Nav =
1.66054 x10-27 kg.
We neglect the mass of the electrons, thus
the mass considered is the mass of the
nucleus.
1 mol of Pu weights 244.0 grams. That is, 1 gram of Pu
contains 1 mol/238.0 nucleus = Nav/238.0 nucleus.
If we consider a mass m (grams) of Pu, then, this mass
corresponds to:
m x Nav/238.0 nucleus.
generally,
The number of nuleus N in a mass of m (grams)
of an element of atomic mass "A"(grams) is:
N = m x Nav/A nucleus
m and A in grams.
3. Density
The density d is equal to m/V.
For a sphere of diameter D, V = (4/3)*π(D/2)3, we
have:
m = d V = d (4/3)*π(D/2)3
And:
N = d (4/3)*π(D/2)3 x Nav/A
A 1 µm diameter sphere of Pu contains:
N = d (4/3)*π(D/2)3 x Nav/A =
19.84 x 103 kg/m3 (4/3)*π(1 x 10-6/2)3 m3
x 6.023 x 1023/238.0 x - 3 kg
= 2.6 x 1010 nucleus.
This ball of Pu is going to decay.
4. α-decays from a Plutonium-238
At time t0 = 0, the number of nucleus that is available is
N0 = 2.6 x 1010 nucleus.
By decaying, the remaining number of nucleus at the
time t is N(t) = N0 exp {- λt}
The half of remaining number of nucleus N0 /2
corresponds to the half-life th:
N0/2 = N0 exp {- λth}
Then: 1/2 = exp {- λth} , hence:
- log 2 = - λ th, thus:
th = log 2 /λ
For the Plutonium-238, we have the half-life th = 88 years
= 88 x 365 x 24 x 60 x 60 seconds = 2.8 x 109 s
Therefore
λ = log 2/ th = 2.50 x 10- 10 s-1
5. Activity of the α-decays from a Plutonium-238
The activity is:
A(t) = - dN(t)/dt = λ N0 exp {- λt} = λ N(t)
The initial activity is A(0) = λ N(0) = λ N0
For the Plutonium-238, A(0) = 2.50 x 10- 10 x 2.6 x 1010 =
6.5 nucleus/s = 6.5 decays/sec = 6.5 Bq
Since:
1 Ci = 3.70 x 1010 Bq =
3.70 x 1010 decays/s,
then:
A(0) = 6.5 Bq = 6.5 Ci /3.70 x 1010 =
1.76 x 10- 10 Ci
If each α emitted has an energy of 5 MeV =
5 x 106 x 1.6 x 10-19 joules =
The activity at t = 1 µs is A(1 µs) =
λ N0 exp {- λ1 µs}
For the Plutonium-238, A(1 µs) =
2.50 x 10- 10 x 2.6 x 1010 exp {- 2.50 x 10- 101 x 10- 6} =
6.5 exp {- 2.50 x 10- 16} = 6.5 x 1 = 6.5 decays/sec = 6.5 Bq
= 6.5 Bq = 1.76 x 10- 10 Ci
6. Dose absorbed and RBE
If each α emitted has an energy of E = 5 MeV =
5 x 106 x 1.6 x 10-19 joules =
8 x 10-13 joules, the dose deposited in a
sphere of 5 µm of diameter in water is:
D = E/V
V = (4/3)π (D/2)3 = (4/3)π (5 x 10-6/2)3
= 6.55 x 10-17 m3
The density of water is equal to 1 kg/dm3 =
1 kg/ -3m3 =
1000 kg/ m3 , d = m/V = 1000 kg/ m3
Therefore:
V (in m3) corresponds to a mass of M = 1000 x V Kilograms =
1000 x 6.55 x 10-17 = 6.55 x 10-14 Kilograms
Therefore:
D = E/M = 8 x 10-13 / 6.55 x 10-14 Joules/Kilograms
= 12.20 Joules/Kilograms
Since:
1 Joule/Kg = 1 Gy
The dose deposited by one α particle of
5 MeV energy due to the decay of a nucleus of Plutonium-238,
in a sphere target of water of 5 µm of diameter is 12.20 Gy.
For this nucleus, we have an activity of A(0) = 6.5 α-decays/second
Then: 6.5 α deposit 6.5 x 12.20 Gy = 79.3 Gy/second
1 year = 365 x 24 x 60 x 60 seconds = 3.15 x 107 s, so:
6.5 α deposit 79.3 Gy/second = 3.15 x 107 x 79.3 Gy/year =
2.50 x 109 Gy/year
Since 1 rad = 0.01 J/kg = 0.01 Gy, we have:
D = 12.20 Joules/Kilograms = 12.20 Gy = 12.20 x 100 rad = 1220.0 rad
All the dose deposited is absorbed., therefore,
the Equivalent dose (rem) = RBE x absorbed dose(rad)
The RBE of α particle = 20 rem/rad
Therefore,
The Equivalent dose (rem) of the one α particle emitted
and absorbed by the sample of water is:
20 x 1220.0 rem = 24400 rem
During a year from the Plutonium sphere, we have
2.50 x 109 Gy/year, that corresponds
to the dose:
Dose = 2.50 x 109 Gy/year = 2.50 x 1011 rad /year =
2.50 x 1011 x 20 rem/year = 5.0 x 1012 rem/year
Terminology:
RBE: Relative Biological Effectiveness
in Sv/Gy = rem/rad
Sv = Sievert
rem = Röntgen equivalent for man
1 Gy (gray) = 1 J/Kg
1 rad = 0.01 Gy
|
|