Mathematics 2: Optimisation linéaire
Examples

Les auberges et les campings

Isa et Franklin préparent à voyager ensemble. Ila planifient de dormir dans des auberges à 20$/nuité et dans des campings à 30$/nuité.

Pour ce voyage, Isa a ses contraintes, Franklin a les siennes.

• Isa ne dispose que de 30 jours au maximum pour ce voyage avec un budget maximal de 600 $. Le nombre de nuits en camping doit être au plus le double de celui dans des auberges.

La différence entre le nombre de nuits dans les auberges et celui en camping de doit pas dépasser 6 nuits.


• Franklin ne dispose pas plus de 24 jours pour ce voyage avec un budget maximal de 750 $. Il veut passer au maximum 3 fois plus de nuits en camping que dans des auberges.

De plus, le nombre de nuits en camping est au moins égal à celui dans des auberges diminué de 4.

Isa et Franklin veulent partir le plus longtemps possible tout en minimisant les dépenses de l'hébergement

Quel est le nombre de nuits qu'ils doivent passer dans chaque type d'hébergement ainsi que le coût de cet hébergement.

x: nombre de nuits à passer dans des aubeges. y: nombre de nuits à passer dans des campings.

Pour Isa • (1) x ≥ 0 • (2) y ≥ 0 • (3) x + y ≤ 30 → y ≤ - x + 30 • (4) 20x + 30y ≤ 600 → y ≤ - (2/3)x + 20 • (5) y ≤ 2x → y ≤ 2x • (6) x - y ≤ 6 → y ≥ x - 6

Pour Franklin • (1) x ≥ 0 • (2) y ≥ 0 • (3) x + y ≤ 24 → y ≤ - x + 24 • (4) 20x + 30y ≤ 750 → y ≤ - (2/3)x + 25 • (5) y ≤ 3x → y ≤ 3x • (6) y ≥ x - 4 → y ≥ x - 4

Le voyage va se faire ensemble, il faut donc que toutes les 12 contrantes d'Isa et de Franklin concordent. Des contraintes (3) d'isa y ≤ - x + 30 et y ≤ - x + 24 de franklin, on retient juste celle de Franklin, puisque ces inégalités ont un même ordre et que le droites correspondantes ont même pente, on retient celle qui a la plus petite ordonnée à l'origine positive . On retient donc y ≤ - x + 24. De même pour (4) y ≤ - (2/3)x + 20 d'Isa et (4) y ≤ - (2/3)x + 25 de Franklin. On retient juste y ≤ - (2/3)x + 20 . De même pour (6) y ≥ x - 6 d'Isa et (6) y ≥ x - 4 de Franklin, on retient celle qui a la plus grande ordonnée à l'origine négative. On retient juste y ≥ x - 4 . Enfin pour (6) y ≤ 2x d'Isa et (6) y ≤ 3x de Franklin, les droites sont linéaires,on retient celle qui a le plus petite pente. On retient donc y ≤ 2x . Ainsi les 12 contraintes se réduisent à 6: • (1) x ≥ 0 • (2) y ≥ 0 • (3) y ≤ - x + 24 • (4) y ≤ - (2/3)x + 20 • (5) y ≥ x - 4 • (6) y ≥ 2x .

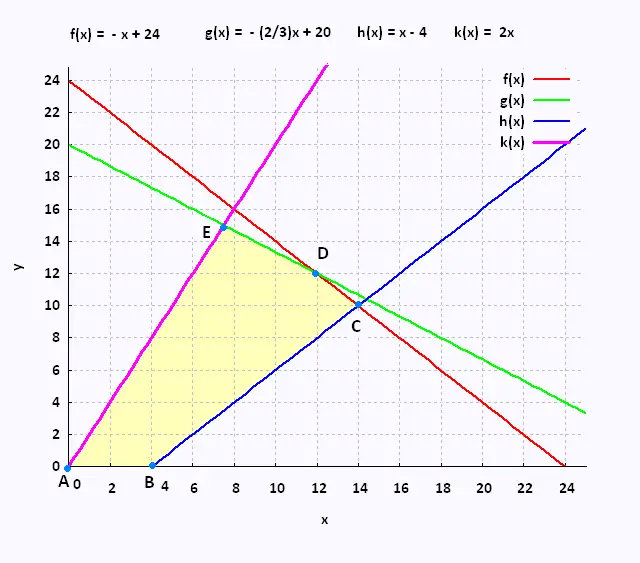
C → f(x) ∩ h(x)    - x + 24 = x - 4 → x = 14 et y = 10    D → f(x) ∩ g(x)    - x + 24 = - (2/3) x + 20 → x = 12 et y = 12    E → g(x) ∩ k(x)    - (2/3) x + 20 = 2x → x = 15/2 et y = 15

Sommets Fonction Z1 (maximiser les jours) = x + y Valeurs de Z1 (jours) Fonction Z2 (minimiser les dépenses) = 20 x + 30 y Valeurs de Z2 ($) A(0, 0) 0 + 0 0 20 (0) + 30 (0) 0 B(4, 0) 4 + 0 4 20 (4) + 30 (0) 80 C(14, 10) 14 + 10 24 20 (14) + 30 (10) 580 *** D(12, 12) 12 + 12 24 20 (12) + 30 (12) 600 E(15/2, 15) = (7,15) par defaut 7 + 15 22 20 (15/2) + 30 (15) 600
		*** : à considérer
Réponse:     Isa et Franklin doivent passer 14 nuits dans des auberges     et 10 nuits dans des campings pour un maximum de 24 jours     et pour un coût total d'herbergement minimum de 580 $.