Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
|
Mathématiques: Algèbre
Optimisation linéaire
Polygone des contraintes
Fonction objectif
Fabrication des bureaux

Une entreprise fabrique deux modèles de bureaux.
Des modèles à deux toroirs et des modèles à quatre tiroirs.
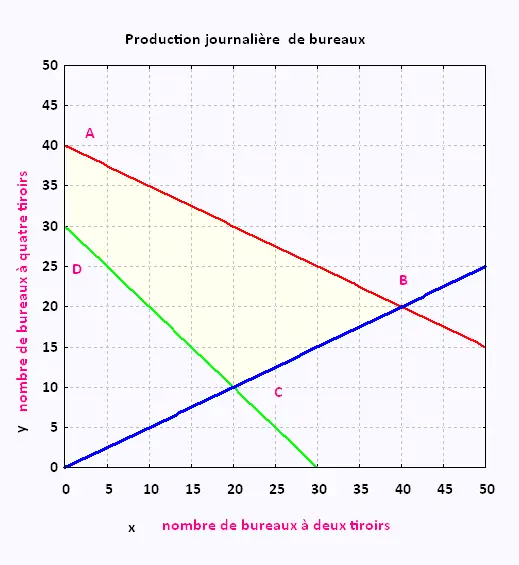
Le fabricant reçoit le rapport suivant contenant le graphique
ci-dessous:
Équations des droites frontières:
2x + 4y = 160
x + y = 30
y = x/2
x = 0
La règle de la fonction à optimiser est C = 80 x + 120 y .
C correspond à au coût de production (en $) des bureaux.
Les coordonnées du point C engendrent la solution optimale.
Exprimer en mots, à l'intention du fabricant, chacune des
contraintes, la règle de la fonction à optimiser et
l'interprétation de la solution optimale.
x : repésente le nombre de bureaux à deux tiroirs.
y : représente le nombre de bureaux à quatre tiroirs.
Selon le polygone des contraintes fourni, le système d'inéquations
est:
2x + 4y ≤ 160
x + y ≥ 30
y ≥ x/2
x ≥ 0
Réponse:
En mots, cela veut dire:
• Le nombre total de tiroirs ne doit pas dépasser 160.
Il faut, au total, un minimum de 30 bureaux.
Le nombre de bureaux à 4 tiroirs doit être au moins
deux fois plus petit que le nombre de bureaux à 2 tiroirs.
Le nombre de bureaux à 4 tiroirs pourrait ne pas être nécessaire.
•
Le coût de production d'un bureau à deux tiroirs est de
80 $. Celui d'un bureau à 4 tiroirs est de 120 $.
On doit donc minimiser les coût global de
fabrication de tous les bureaux.
Il ya un nombre optimal de bureaux de chaque modèle à fabrique afin de
minimiser les coûts de production. Il est de 20 pour les bureaux
à deux troirs et de 10 pour les bureaux à quatre troirs.
• Ainsi pour minimiser les coûts de
production à 80(20) + 120(10) = 2800 $, il convient de fabriquer
20 bureaux de modèle 2 tiroirs et 10 bureaux de modèle 4 tiroirs.
|
|