Mathematics 2: Optimisation linéaire
Examples

Camion poids lourd

Un camion poids lourd transporte des boîtes de masse 150 kg et des boîtes de masse 100 kg, toutes de même dimensions.

La charge que peut transporter le camion ne doit pas dépasser 24 tonnes.

Le nombre maximum de boîtes que peut transporter le camion est 200 boîtes.

Le transport d'une boîte de masse 150 kg rapporte 25 $. Clui d'une boîte de masse 100 kg rapporte 20 $.


Combien de boîtes de chaque sorte doit-on transporter pour maximiser les revenus?

1 tonne = 1000 kg.

x: nombre de boîtes de masse 150 kg.

y: nombre de boîtes de masse 100 kg.

• x ≥ 0 • y ≥ 0 • x + y ≤ 200 → y ≤ - x + 200		• 150 x + 100 y ≤ 24 000 → y ≤ - 1.5 x + 240 • ...........................................
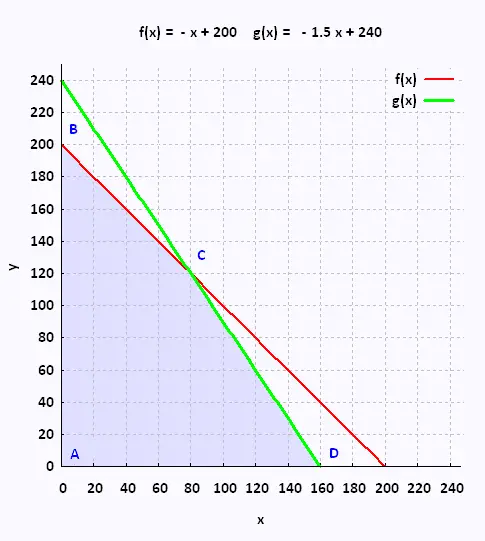
		C → f(x) et g(x)    ...........................................    ...........................................    - x + 200 = - 1.5 x + 240 → x = 80 y = 120    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................
Sommets Fonction Z = 25 x + 20 y Valeurs de Z A(00, 30) 25 (0) + 20 (0) 0 B(0, 200 25 (0) + 20 (200) 4000 C(80, 120) 25 (80) + 20 (120) 4400 *** C(160, 0) 25 (160) + 20 (0) 4000
		*** : à considérer
Réponse:     Pour un profit maximum de 14400 $, on doit     transporter 80 boîtes de 150 kg et 120 boîtes de masse 100 kg.