Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
| Mathematics 2: Linear optimization
Examples
Chocolate

A company manufactures two kinds of
chocolate bars with two principal
ingredients: chocolate and milk.
Kind A : bar of 100 g chocolate and 25 g milk,
which costs 4.00 $.
Kind B : bar of 150 g chocolate and 10 g milk,
which costs 6.00 $.
The available quantities of chocolate and milk
are 30 kg and 5 kg respectively.
How many bars of each kind the company would
produce to maximize its profit ?
Set the unknown:
x is the number of bars of kind A
y is the number of bars of kind B
kind A : 100 x g of chocolate and 25 x g of milk
kind B : 150 y g of chocolate and 10 y g of milk
Thus
100 x + 150 y g of chocolate, and
25 x + 10 y g of milk.
100 x + 150 y ≤ 30 000
25 x + 10 y ≤ 5 000
Or
(1) 2 x + 3 y ≤ 6 00
(2) 5 x + 2 y ≤ 1 000
Function objective: Z = 4 x + 6 y : maximum
We graph the following equations:
(1) y = - (2/3) x + 200
(2) y = - (5/2) x + 500
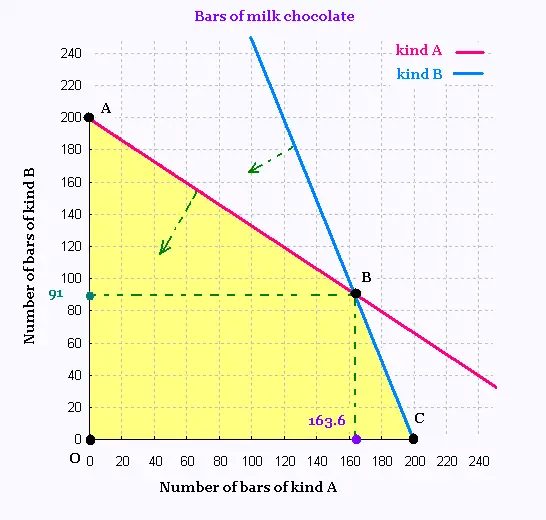
Let's find the coordinates of the point B of the intersection
of the two lines (1) and (2):
Equating the two related equations gives:
- (2/3) x + 200 = - (5/2) x + 500
Solving for x leads to the following repeating decimals:
x = 1800/11 = 163.63 and
y = 1000/11 = 90.90.
The value of the function objective Z is then:
Z = 4 (1800/11) + 6 (1000/11) = 1200.00 (an exact value)
Note that x is the number of bars of kind A and y is the number of bars of kind B.
These numbers connot be, in this contexte, decimal numbers. We need to
round them.
We cannot round up the values of x and y, because we will need more the given
ingredients (both choclate and milk).
Rounding down, we get:
x = 163 and y = 90.
The value of the function objective Z is then:
Z = 4 (163) + 6 (90) = 1192.00 .
In this case the related loss is: 1200.00 - 1192 = 8 $
We should accept this loss if we didn't have a better choice.
We have the better choice with the point (0,200).
| Vertex | Z ($) |
| (0, 0) | 0 |
| (0, 200) | 1200 *** |
| (163, 90) | 1192 → loss 8 $. |
| (200, 0) | 800 |
To obtain the maximum profit which is 1200.00 $,
the company would produce 200 bars of chocolate-milk
of kind B without producing any of kind B.
|
|