Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
| Mathematics 2: Linear optimization
Examples
Crescents

A baker makes two types of crescents:
He has 20 kg of butter, 4 kg
sugar, and 2 kg of egg yolk (100 eggs).
Type A : extra butter:
840 g butter,
100 g of sugar,
40 g egg yolk.
This recipe produces 10 crescents, $ 15
each.
Type B extra eggs:
600 g butter,
120 g of sugar,
80 g egg yolk
This recipe produces 10 crescents, $ 18
each.
How many of each kind of recipes
the baker must make to have a
maximum profit. What is this profit?
x number of recipes A
y number of recipes B
Butter: 840 x + 600 y = 20,000
Sugar: 100 x + 120 y = 4000
Yolk: 40 x + 80 y = 2000
(1): 21x + 15y = 500
(2): 5x + 6y = 200
(3): x + 2y = 50
(1): y = - 7x/ 5 + 100/3
(2): y = - 5x/ 6 + 100/3
(3): y = - x/ 2 + 25
Z = 15 x + 18 y maximum
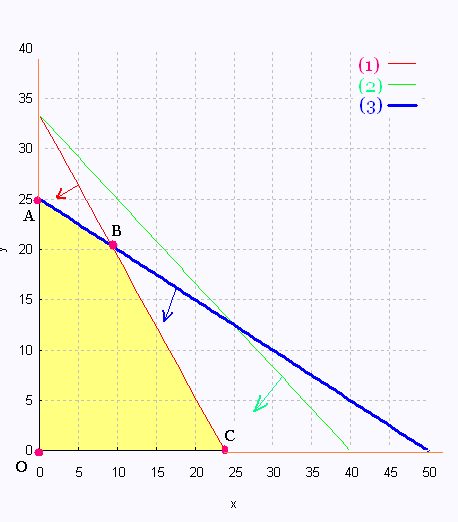 The 4 vertices are:
1. O(0,0)
2. A(0, 25)
3. C(500/21,0)
The 4 vertices are:
1. O(0,0)
2. A(0, 25)
3. C(500/21,0)
4. Let's find the coordinates of the point B of the intersection
of the two lines (1) and (3):
Equating the two related equations gives:
- 7x / 5 + 100/3 = - x/2 + 25
Solving for x leads to the following repeating decimals:
x = 250/27 = 9.259 and
y = 550/27 = 20.370.
The value of the function objective Z is then:
Z = 15 (250/27) + 18 (550/27 ) = 4550/9 = 505.5
Note that x number of recipes A, and y number of recipes B.
These numbers connot be, in this contexte, decimal numbers. We need to
round them.
We cannot round up the values of x and y, because we will need more the given
ingredients.
Rounding down, we get:
x = 9 and y = 20.
The value of the function objective Z is then:
Z = 15 (9) + 18 (20) = 495.00 $.
In this case the related loss is: 4550/9 - 495 = 95/9 = 10.5 $
We have to accept this loss we don't have a better choice.
| Vertex | Z ($) |
| (0, 0) | 0 |
| (500/21, 0) | 357.14 |
| (9, 20) | 495 $ *** → loss: 10.5 $ |
| (0, 25) | 450 |
To obtain the maximum profit, which is 495 $, along with a loss of
about 11 $, the baker will make 9 recipes of crescent type A and
20 recipes of crescent type B.
|
|