Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
|
Mathematics 2: Optimisation
linéaire
Examples
Embouteillage d'eau potable

Une entreprise de boissons dispose d'au plus de 1800 litres d'eau pure
à embouteiller.
Deux types de bouteilles sont utilisés: des bouteilles de 6 litres et des
bouteilles de 10 litres.
On dispose d'au moins 5 fois plus de bouteilles de 6 litres que de 10 litres,
et il ya au moins 15 bouteilles de 10 litres disponibles.
Au total, on estime qu'au moins 1200 litres d'eau devront être
embouteillées
Le coût de l'embouteillage d'un contenant de 6 litres est de
2.00 $ et celui d'un contenant de 10 litres est de 3.00 $
Quel est le nombre de bouteilles de chaque sorte doit utiliser
afin de minimiser le coût relié à l'embouteillage de l'eau?
|
x: nombre de bouteilles de 6 litres.
|
|
y: nombre de bouteilles de 10litres.
|
• x ≥ 0
• y ≥ 0
• 6x + 10y ≤ 1800 →
y ≤ - 3x/5 + 180
|
•
y ≥ 15
• 6x + 10y ≥ 1200 →
y ≥ - 3x/5 + 120
• x ≥ 5 y →
y ≤ x/5
|
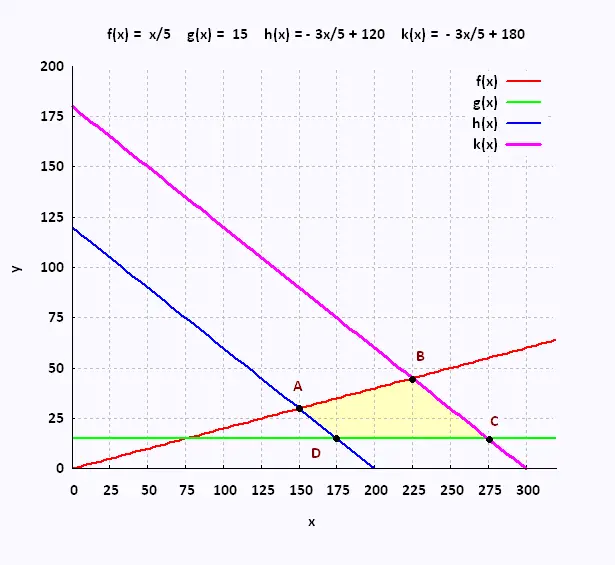
|
A → f(x) et h(x)
...........................................
x/5 = - 3x/5 + 120 → x = 150 y = 30
...........................................
B → f(x) et k(x)
...........................................
x/5 = - 3x/5 + 180 → x = 225 y = 45
...........................................
C → g(x) et k(x)
...........................................
15 = - 3x/5 + 180 → x = 275 y = 15
...........................................
D → g(x) et h(x)
...........................................
15 = - 3x/5 + 120 → x = 175 y = 5
...........................................
|
| Sommets | Fonction Z = 2 x + 3 y | Valeurs de Z |
| A(150, 30) | 2(150) + 3(30) | 390 *** |
| B(225, 45) | 2(225) + 3(45) | 585 |
| C(275, 15) | 2(275) + 3(15) | 595 |
| D(175, 15) | 2(175) + 3(15) | 395 |
|
| |
*** : à considérer
|
Réponse: Pour minimiser les coûts
liées à l'embouteillage de l'eau à 390 $,
on doit utiliser 150 bouteilles de 6 litres et 30
bouteilles de 10 litres.
|
|
|