Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
|
Mathematics 2: Optimisation linéaire
Examples
La fleuriste

Carmen cultive et vend des iris et des oeillets. Elle en compose
des bouquets de deux sortes.
Le coût de production d'un bouquet formé d'iris est de
7.00 $ et est vendu à 11.00 $. Le coût de production d'un bouquet
formé d'oeillets est de 4.00 $ et est vendu à 9.00 $.
La fleuriste veut avoir des revenus d'au moins 3200 $ avec
la vente de ses fleurs. Le coût de production doit être d'au plus
1800 $.
Combien de fleurs de chaque sorte Carmen doit-elle produire pour maximiser
le nombre de fleurs sur le marché?
|
x: nombre de bouquets d'iris
|
|
y: nombre de bouquets d'oeillets
|
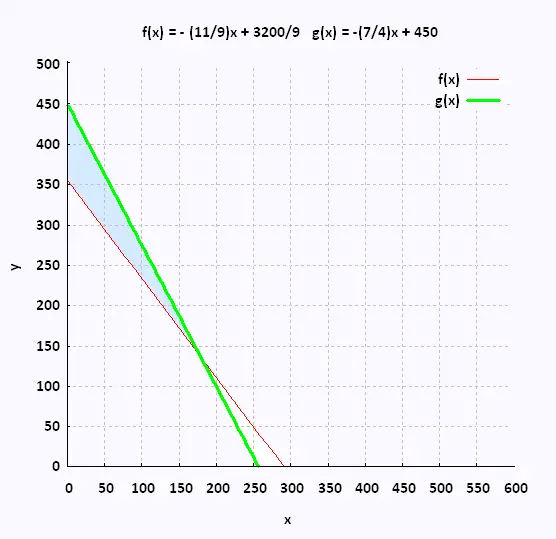
• x ≥ 0
• y ≥ 0
• 11 x + 9 y ≥ 3200 →
y ≥ - (11/9) x + 3200/9
|
• 7 x + 4 y ≤ 1800 →
y ≤ - (7/4)x + 450
• ...........................................
• ...........................................
|
|
- (11/9)x + 3200/9 = - (7/4)x + 1800/4
...........................................
(7/4 - 11/9)x = 1800/4 - 3200/9
...........................................
x (63 - 44) = 16200 - 12800
...........................................
x = 3400/19 = 179
...........................................
y = 137
...........................................
...........................................
...........................................
...........................................
|
| Sommets | Fonction Z = x + y | Valeurs de Z |
| A(0,355.56) | // | // |
| B(0,450) | 0 + 450 | 450 |
| C(179,137) | // | // |
|
Réponse: Carmen doit composer 450 bouquets d'oeillets
et aucun bouquet d'iris.
|
|
|