Mathematics 2: Optimisation linéaire
Examples

Le joaillier

Un joallier vend des bagues de diamant et des bagues de zircon.

Il ne doit pas garder en magasin plus de 60 bagues. Mais il doit en avoir au moins 30.

Les bagues de diamant sont au moins deux fois plus demandées que celles de zircon.

Une bague de diamant permet de faire 50 $ de profit. Celle du zircon 75 $.

Combien de bagues de chaque sorte doit-on vendre pour maximiser le profit?

x: nombre de bagues de diamant.

y: nombre de bagues de zircon.

• x ≥ 0 • y ≥ 0 • x + y ≤60 → y ≤ - x + 60		• x + y ≥ 30 → y ≥ - x + 30 • x ≥ 2 y → y ≤ x/2 • ...........................................
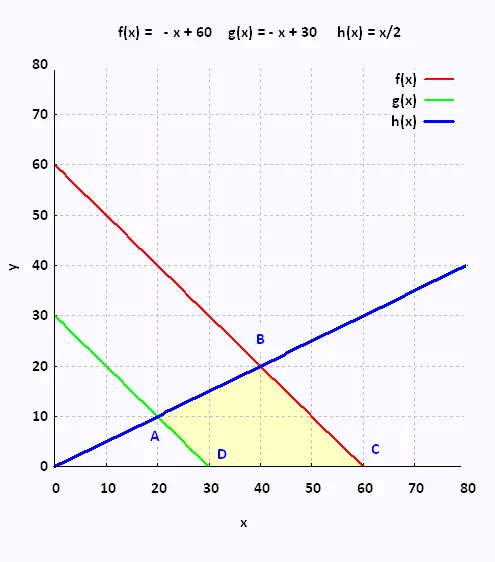
		A → g(x) et h(x)    ...........................................    - x + 30 = x/2 → x = 20 y = 10    ...........................................    ...........................................    B → f(x) et h(x)    ...........................................    - x + 60 = x/2 → x = 40 y = 20    ...........................................    ...........................................    ...........................................    ...........................................
Sommets Fonction Z = 50 x + 75y Valeurs de Z A(20, 10) 50 (20) + 75 (10) 1750 B(40, 20) 50 (40) + 75 (20) 3500 *** C(60, 0) 50 (60) + 75 (0) 3000 C(30, 0) 50 (30) + 75 (0) 1500
		*** : à considérer
Réponse:     Pour un profit maximum de 3500 $, le joallier     doit vendre 40 bagues en diamant et 20 bagues en zircon.