Mathematics 2: Optimisation linéaire
Examples

Les motos

Bill offre à sa clientèle des motocyclettes neuves et usagées.

Par mois, Il doit vendre au moins 35 motos. Il doit aussi vendre par mois au moins 10 motos neuves de plus que les motos usagées.

Le nombre de motos en vente ne peut pas dépasser 65 par mois.

À la vente, Bill reçoit 400 $ par moto neuve et 200 $ par moto usagée.

Combien de motos de chaque sorte doit-il vendre pour maximiser son revenu ?

x: nombre de motos neuves

y: nombre de motos usagées

• x ≥ 0 • y ≥ 0 • x + y ≥ 35 → y ≥ - x + 35		• x ≥ 10 + y → y ≤ x - 10 • x + y ≤ 65 → y ≤ - x + 65 • ...........................................
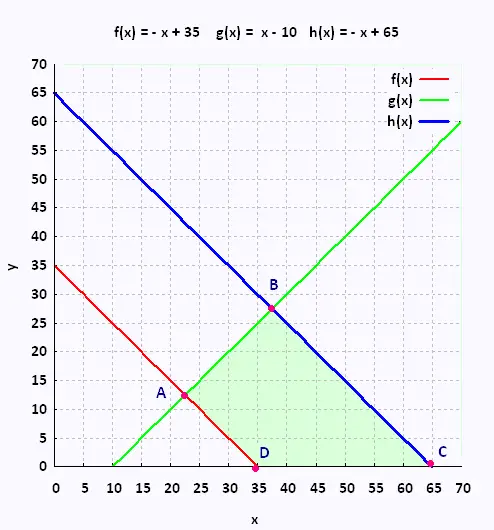
		A → f(x) et g(x)    ...........................................    - x + 35 = x - 10 → x = 22.5 y = 12.5    ...........................................    ...........................................    B → g(x) et h(x)    ...........................................    x - 10 = - x + 65 → x = 37.5 y = 27.5    ...........................................       ...........................................    ...........................................    ...........................................    ...........................................
Sommets Fonction Z = 400 x + 200 y Valeurs de Z A(22.5,12.5) 400 (22.5) + 200 (12.5) 11500 // B(37.5,27.5) 400 (37.5) + 200 (27.5) 20500 // C(65,0) 400 (65) + 200 (0) 26 000 *** D(35,0) 400 (35) + 200 (0) 14 000
// (décimaux) à rejeter		*** : à considérer
Réponse:     Bill doit vendre 65 motos neuves     et aucune moto usagée pour un revenu de 26 000 $.