Mathematics 2: Linear optimization
Examples

Directement de la ferme

Achetées directement de la ferme, une caisse d'haricots de 30 kg coûte 150 $ et une caisse de pomme de terre de 40 kg coûte 100 $.

Un commerçant dispose de 2100.00 $ pour acheter ces légumes. Avec son camion, il peut rapporter une charge de dépassant pas 600 kg.

Le commerçant réalise un profit de 65 $ sur la vente d'une caisse d'haricots et de 40 $ sur la vente d'une caisse de pommes de terre.

Combien de caisse de chaque sorte le commerçant devra-t-il rapporter pour maximiser ses profits ?

x: nombre de caisses d'haricots.

y: nombre de caisse de pommes de terre.

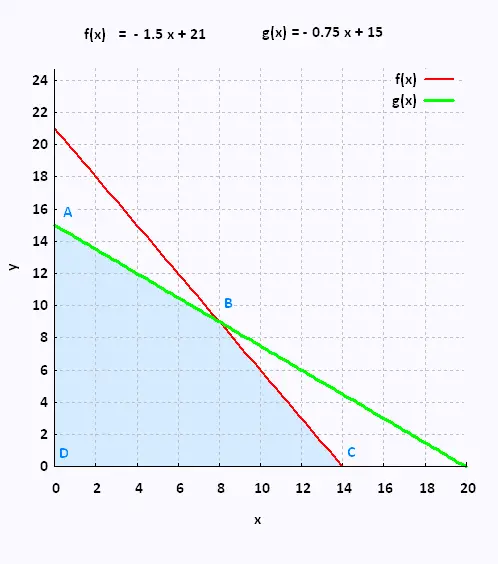
• x ≥ 0 • y ≥ 0 • 150 x + 100 y ≤ 2100 → y ≤ - 1.5 x + 21		• 30 x + 40 y ≤ 600 → y ≤ - 0.75 x + 15 • ...........................................
		B → f(x) et g(x)    ...........................................    - 1.5 x + 21 = - 0.75 x + 15 → x = 8 y = 9    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................    ...........................................
Sommets Fonction Z = 65 x + 40 y Valeurs de Z A(0, 15) 65 (0) + 40 (15) 600 B(8, 9) 65 (8) + 40 (9) 880 C(14, 0) 65 (14) + 40 (0) 910 *** C(0, 0) 65 (0) + 40 (0) 0
		*** : à considérer
Réponse:     Pour un profit maximum de 910 $, on doit     rapporter 14 caisses d'habricots et aucune caisse de pommes de terre.