Mathematics 2: Optimisation linéaire
Examples

Les pots de miel

Diane est une apicultrice. Par l'élevage d'abeilles, elle produit du miel pour faire un revenu.

Elle verse le miel récolté dans des contenants de formats 1 litre et 3 litres.

Par cet élevage, elle produit au moins 60 litres de miel.

Le premier format est au moins trois fois plus demadé que le second.

La production ne dépasse pas 60 contenants.

Le contenant d'un litre est vendu à 8.00 $. Le contenant de trois litres est vendu à 20 $.

Quel est le nombre de contenants de chaque format qui vont lui permettre de réaliser un profit maximal ?

x: nombre de contenants d'un litre

y: nombre de contenants de trois litres

• x ≥ 0 • y ≥ 0 • x + 3y ≥ 60 → y ≥ - x/3 + 20		• x ≥ 3 y → y ≤ x/3 • x + y ≤ 60 → y ≤ 60 - x • ...........................................
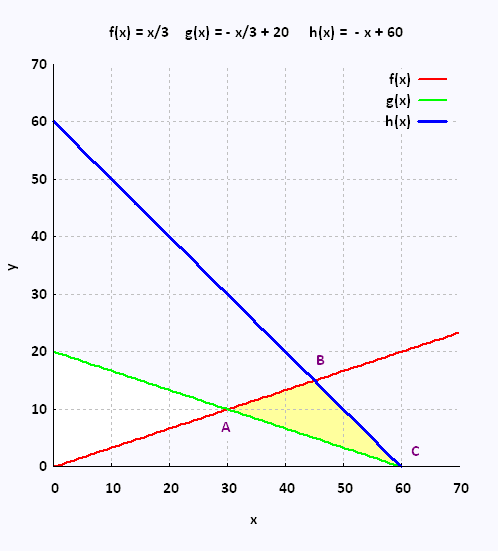
		A → f(x) et g(x)    ...........................................    x/3 = - x/3 + 20 → x = 30 y = 10    ...........................................    A(30, 10)    ...........................................    B → f(x) et h(x)    ...........................................    x/3 = - x + 60 → x = 45 y = 15    ...........................................    B(45, 15)    ...........................................
Sommets Fonction Z = 8 x + 20 y Valeurs de Z A(30, 10) 8(30) + 20(10) 440 B(45, 15) 8(45) + 20(15) 660 *** C(60, 0) 8(60) + 20(0) 480
		*** : à considérer
Réponse:     Diane produira 45 contenants d'un litre et     15 contenants de 3 litres pour un revenu maximum de 660 $.