Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
| Mathematics 2: Linear optimization
Examples
Balanced diet

Jim weights 72.5 kg. To balance his
diet, he needs daily, en average, 80 g
of protein, 300 g of carbohydrates (carb),
and 88 g of lipids (fat).
He will take just cheese and seedless
raisins along a day, by using two recipes:
1. Nutrient 1:
100 g Cheddar Cheese nutrition facts:
Protein: 33 g
Carb: 2 g
Fat: 44 g
Price: 4.00$
and
2. Nutrient 2:
100 g Seedless raisins nutrition facts:
Protein: 3 g
Carb: 79 g
Fat: 1 g
Price: 1.00$
How many grammes of each nutrient Jim
will buy to maintain a balanced diet and
pay less.
x is the number of nutrient 1, and
y is the number of nutrient 2.
(1) 33 x + 3 y ≥ 80
(2) 2 x + 79 y ≥ 300
(3) 44 x + y ≥ 88
(1) y = - 11 x + 80/3
(2) y = - 2/79 x + 300/79
(3) y = - 44 x + 88
Z = 4 x + 1 y min
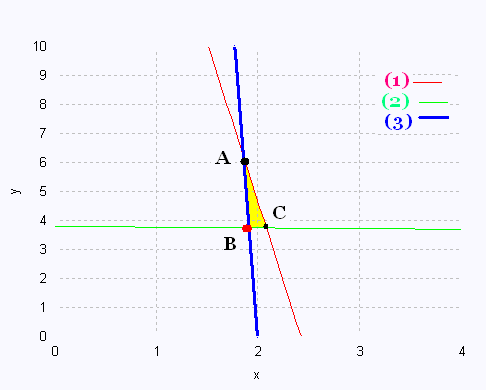
The 3 vertices are:
1. A(1.86,6.22)
- 11 x + 80/3 = - 44 x + 88
x = 1.86
y = 6.22
2. B(1.92, 3.70)
- 2/79 x + 300/79 = - 44 x + 88
x = 1.92
y = 3.70
3. C(2.10, 3.67)
- 11 x + 80/3 = - 2/79 x + 300/79
x = 2.10
y = 3.67
| Vertex | Z ($) |
| (1.86, 6.22) | 13.74 |
| (1.92, 3.70) | 11.38 |
| (2.10, 3.67) | 12.07 |
To obtain the minimum price to pay, which is 11.38 $, Jim
will take 1.92 x 100 g = 192 g of Cheddar cheese ,
and 3.70 x 100 g = 370 g of raisins to keep
a balanced diet for one day.
|
|