Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
| Mathematics 2: Linear optimization
Examples
Honey

Albert sells three kinds of honey. Buckwheat,
clover, and wildflower. He has no clover honey in
stock. The Buckwheat honey is sold in 2-lbs
bottles with 10 $, the wildflower honey is
sold in 1-lb bottles with 12 $. He needs at
least 200 bottles to sell at most 380 lbs of
honey, with at least 2 times 2-lbs bottles
more than 1-lb bottles.
What is the maximum
profit can Albert hope ?
Step 1: Identify the variables x, y
Step 2: formulate constraints and make the graph
Step 3: find vertices
Step 4: Write the equation to maximize profit
Step 5: Complete the table
Step 6 :formulate the answer
step 1 :
x : number of 1-lb bottles
y : number of 2-lbs bottles
x ≥ 0
y ≥ 0
(1) x + y ≥ 200
(2) x + 2y ≤ 380
(3) y ≥ 2x
Step 2:
We translate the five constraints in a Cartesian
plane.
Using the above inequality, we identify the polygon
of constraints that will contain all the areas of each
constraints.
Isolate the variables y in the three equations (1),
(2), and (3):
(1) y ≥ - x + 200
(2) y ≤ - x/2 + 190
(3) y ≥ 2x
Plot the graph:
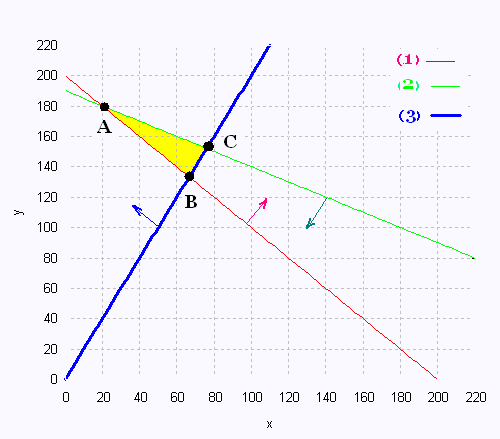
The vertices of the polygon of constraints
determine the minimum or maximum value of the
function to be optimized. Comparison method will
be useful to find some vertices.
From the polygon of constraints, we consider the
three vertices. We will work with the equalities:
Vertex A:
This is the point of intersection between
the constraints (1) and (2).
- x + 200 = - x/2 + 190
x = 20 and y = 180
The coordinates of the vertex A are (20, 180)
Vertex B:
This is the point of intersection between
the constraints (1) and (3).
- x + 200 = 2x
x = 200/3 = 66.67 y = 400/3 = 133.33
The coordinates of the vertex B are (66.67 , 133.33)
Vertex C:
This is the point of intersection between
the constraints (2) and (3).
- x/2 + 190 = 2x
x = 76 , y = 152
The coordinates of the vertex C are (76 , 152)
Step 4:
We write the equation that will use the found vertices
and thus answer the question of the problem.
We want the maximum profit:
The function objective Z is
Z = 12 x + 10 y
Step 5:
In a table, we use the function to optimize Z
and perform a calculation using each found vertex.
| Vertex | Z ($) |
| (20, 180) | 2040 |
| (66.67, 133.33) | 2133.34 |
| (76 , 152) | 2432 |
Step 6:
We find one maximum value to maximize the profit.
It is 2432 $.
Answer: To get the maximum benefit, Albert will use
76 1-lb bottles, and 152 2-lbs bottles.
|
|