Mathematics 2: Linear optimization
Examples

Jean pants

A plant produces two kinds of jean pants : Jean A and Jean B.

A made jean pants passes through three machines:

Machine M1: cut the fabric. It operates at most 5 hours,
Machine M2: sew the pants. It operates at most 4 hours,
Machine M3: install rivets. It operates at most 2 hours.

• Jean A:
It costs 50.00 $.
The Machine M1 spends 5 mn to cut its fabric, the Machine M2 spends 6 mn to sew the pants, and the Machine M3 spends 8 mn to install special rivets.

• Jean B:
It costs 30.00 $.
The Machine M1 spends 3 mn to cut its fabric, the Machine M2 spends 5 mn to sew the pants, and the Machine M3 spends 2 mn to install rivets.

How many jean pants the factory should produce to maximize its profit?

Solution

Set the unknown:

x is the number of jean pants of kind A
y is the number of jean pants of kind B

The operation time (in mn) for the three machines:

M1: 5 x + 3 y ≤ 5 x 60 = 300
M2: 6 x + 5 y ≤ 4 x 60 = 240
M3: 8 x + 2 y ≤ 2 x 60 = 120

The equivalent equations are:

M1: y = - (5/3) x + 100
M2: y = - (6/5) x + 48
M3: y = - 4 x + 60

Their graph is:



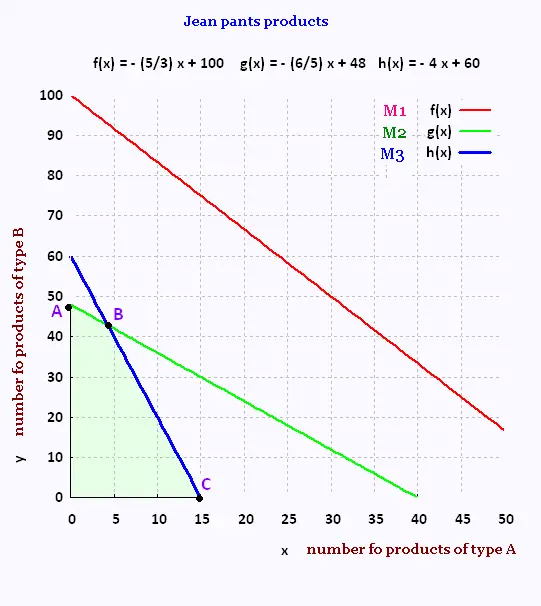
Function objective Z = 50 x + 30 y Maximum

Vertex	Z ($)
O(0, 0)	0
A(0, 48)	1440
B(4.3, 42.86)     →     B(4, 42)	1505
C(15,0)	750

To obtain the maximum profit which is 1505 $, the factory would produce 4 jean pants of kind A and 42 jean pants of kind B.