Mathematics 2: Linear optimization
Examples

Juices

A company produces juices in three different types: orange juice, strawberry juice, and apple juice. It will be produced at least 1000 orange juice bottles, at least 2000 strawberry juice bottles, and at least 3500 apple juice bottles. The company has two bottling plants.

Each day,
• the first plant produces:
50 orange juice bottles
60 strawberry juice bottles
70 apple juice bottles

• the second plant produces:
40 orange juice bottles
50 strawberry juice bottles
70 apple juice bottles

a) The operating expenses are 800 $ for each plant each day.
For how long should each plant run to meet the needs and to maintain a minimum cost?

b) Now, the operating expenses are 600 $ and 400 $ each day for the first plant and for the second plant respectively. For how long should each plant run to meet the needs and to maintain a minimum cost?

step 1 :
x : the number of days of operation for the first plant, 
y : the number of days of operation for the second plant

x ≥ 0
y ≥ 0

Plant 1: 
The first plant will produce: 
50 x  orange juice bottles
60 x  strawberry  juice bottles
70 x  apple juice bottles
800 x $

Plant 2: 
The second plant will produce: 
40 y orange juice bottles
50 y strawberry juice bottles
70 y apple juice bottles
800 x $

50 x + 40 y > 1000 
60 x + 50 y > 2000 
70 x + 70 y > 3500 

Step 2:

We translate the five constraints in a Cartesian 
plane. 
Using the above inequality, we identify the polygon 
of constraints that will contain all the areas of each
constraints.

Isolate the variables y in the three equations (1), 
(2), and (3):

(1) y > - 5x/4 + 25
(2) y > - 6x/5 + 40 
(3) y > - x + 50 

Plot the graph: 



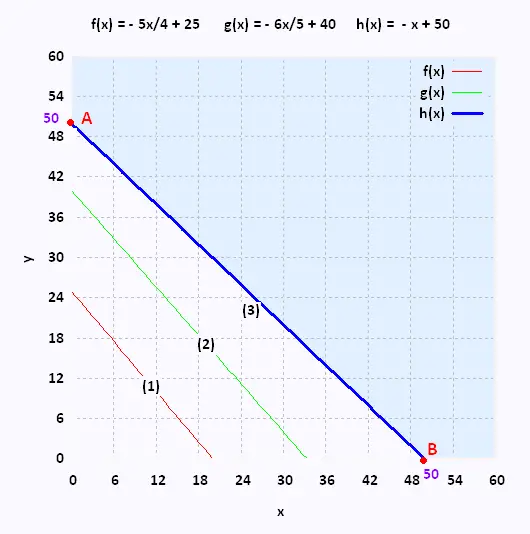The vertices of the polygon of constraints 
determine the minimum or maximum value of the 
function to be optimized. 

From the polygon of constraints, we consider the 
two vertices given by the equation: y = - x + 300/7.
 
Vertex A: (0,50)
Vertex B: (50,0)

Step 4:
We write the equation that will use the found vertices 
and thus answer the question of the problem.
We want the maximum profit:

The function objective Z is 

Za = 800 x $ + 800 y $ minimum
Zb = 600 x $ + 400 y $ minimum

Step 5:
In a table, we use the function to optimize Z 
and perform a calculation using each found vertex.



Vertex 
			Za ($)
 
			Zb ($)
(0, 50)	
	40,000 
 
			20,000
(50, 0) 
 40,000
 
			30,000


Step 6:
We find the values to minimize the related cost: 

0 days for the plant 1 and 50 days for the plant 2 .
50 days for plant 1, 0 days for the plant 2.
The minimum cost is 20,000 $.

Answer: To get a minimum , the plant 2 will run 
50 days with the operating expenses of 400 $.