Linear
optimization
Optimisation
linéaire
Avec Solveur d'Excel
MS Office
© The scientific sentence. 2010
| Mathematics 2: Linear optimization
Examples
Milk factory

A dairy farmer wants to produce daily at least 150 liters of skimmed milk, 300 liters of 2% milk and 800 liters of whole milk. He has two factories where to pasteurize and to bottle milk.
The first factory "A" pasteurizes and bottles 10 liters of skimmed milk, 40 liters of 2% milk and 180 liters of whole milk. The related operating expenses costs 150 $.
The second factory "B" pasteurizes and bottles 40 liters of skimmed milk, 50 liters of 2% milk and 90 liters of whole milk. The related operating expenses costs 250 $.
For how many days, should the former run both
factories to minimize the production costs while
satisfying the given constraints?
Solution
Set the unknown:
x is the number of operating days of the factory A
y is the number of operating days of the factory B
A: 40 x liters of skimmed milk, 50 x liters of 2% milk and 90 x liters of whole milk.
B: 10 y liters of skimmed milk, 40 y liters of 2% milk and 180 y liters of whole milk.
The productions and the constraints are:
40 y + 10 x ≥ 150
50 y + 40 x ≥ 300
90 y + 180 x ≥ 800
Or
The equivalent equations are:
y = - x/4 + 15/4
y = - 4 x/5 + 30/5
y = - 2 x + 80/9
Their graph is:
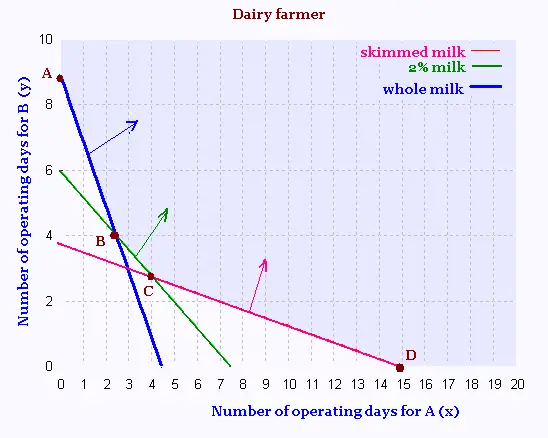
Vertex B:
- 4 x/5 + 30/5 = - 2 x + 80/9
x = 2.41, and y = 4.07
Vertex C:
- x/4 + 15/4 = - 4 x/5 + 30/5
x = 4.1, and y = 2.71
Function objective Z = 150 x + 250 y Minimum.
| Vertex | Z ($) |
| A(0, 80/9) | 2222.22 |
| B(2.41, 4.07) | 1373.5 |
| C(4.1,2.71) | 1292.5 |
| D(15,0) | 2250 |
To obtain the minimum operating expenses that are 1292.5 $, the factory "A" would operate 4.1 hours = 4h 6mn, and the factory "B" 2.71 hours = 2h 43mn to minimize the opertaing expenses.
|
|