Uncertainty on the slope and they-intercept
1. Maximum values for two points
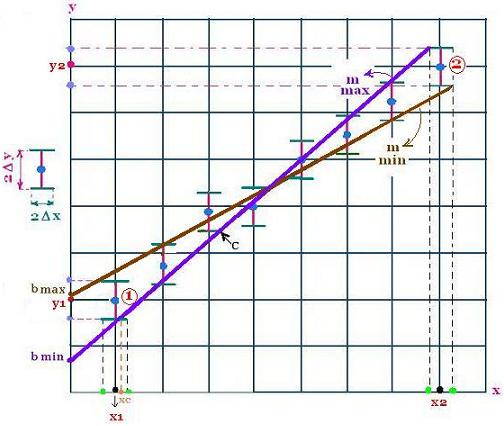 From the graph, we consider the highest point 2(x2,y2) and
the lowest point 1(x1,y1), and the rectangle (2Δx) (2Δy )
around each point.
From the graph, we consider the highest point 2(x2,y2) and
the lowest point 1(x1,y1), and the rectangle (2Δx) (2Δy )
around each point.
Therefore:
y2 max = y2 + Δy and y2 min = y2 - Δy
y1 max = y1 + Δy and y1 min = y1 - Δy
x2 max = x2 + Δx and x2 min = x2 - Δx
x1 max = x1 + Δx and x1 min = x1 - Δx
2. The expression of the slope: m
mmax = [(y2 + Δy) - (y1 - Δy)]/[(x2 - Δx) - (x1 + Δx) ]
mmax = [(y2 + Δy) - (y1 - Δy)]/[(x2 - Δx) - (x1 + Δx) ]
Here:
Δx = xc because we have constraint in the point C.
Similarly,
mmin = [(y2 - Δy) - (y1 + Δy)]/[(x2 + Δx) - (x1 - Δx) ]
mmin = [(y2 - Δy) - (y1 + Δy)]/[(x2 + Δx) - (x1 - Δx)]
Now, we determine Mm nad Δm:
Mm = (mmax + mmin)/2
= [(y2 - y1)(x2 - x1) + (4Δx Δy)]/[(x2 - x1)2 - 4 Δx2]
And
Δm = (mmax - mmin)/2
= [2(x2 - x1)Δy + 2(y2 - y1)Δx ]/[(x2 - x1)2 - 4 Δx2]
mmin = [(y2 - Δy) - (y1 + Δy)]/[(x2 + Δx) - (x1 - Δx)]
mmin = [(y2 - Δy) - (y1 + Δy)]/[(x2 + Δx) - (x1 - Δx)]
Mm = (mmax + mmin)/2
Δm = (mmax - mmin)/2
3. The expression of the y-intercept: b
2.1. Using the slope m max:
[(y2 + Δy) - bmin ]/[(x2 - Δx) - 0] = slope = mmax
That is:
[(y2 + Δy) - bmin ] = (x2 - Δx) mmax, or
bmin = (y2 + Δy) - (x2 - Δx) mmax
Similarly,
2.2. Using the slope m min:
[(y2 - Δy) - bmax ]/[(x2 + Δx) - 0] = slope = mmin
That is:
[(y2 - Δy) - bmax ] = (x2 + Δx) mmin,
or
bmax = (y2 - Δy) - (x2 + Δx) mmin
bmin = (y2 + Δy) - (x2 - Δx) mmax
bmax = (y2 - Δy) - (x2 + Δx) mmin
Now, we determine Mb and Δb:
Mb = (bmax + bmin)/2
= y2 - x2 (Mm) + Δx Δm ,
Δb = (bmax - bmin)/2
= - Δy + x2Δm - Δx (Mm)
Mb = (bmax + bmin)/2
= y2 - x2 (Mm) + Δx Δm
Δb = (bmax - bmin)/2
= - Δy + x2Δm - Δx (Mm)
The y-intercept is written as:
b = Mb ± Δb
4. The equqtion y = (slope) x + Y-interecept
Using the above results, the equation of
the related line is:
y = b + m t
= (Mb ± Δb) + (Mm ± Δm)t
y = b + m t
= (Mb ± Δb) + (Mm ± Δm)t
Get your related calculations here: Uncertainty calculator .
|