Physique 23 : Electricité et magnétisme
Champ magnétique
Force de laplace

1. Poids partiel sur un plan incliné

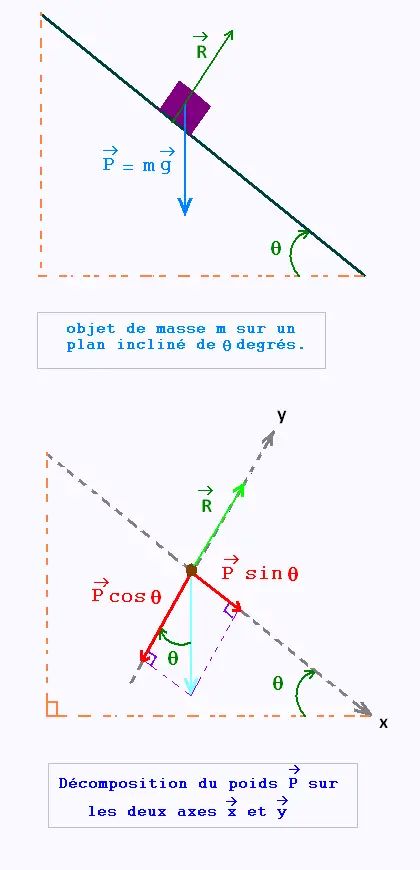
Sur un plan incliné, un objet de masse m est soumis à son poids et à la réaction du plan sur lui.
On choisit un axe, l'axe des x, parallèle au plan incliné et un deuxième axe, l,axe des y, perpendiculaire au premier.

On projette le poids et la réaction sur ses axes, on obtient deux equations:

• Sur l'axes des y: R - mg cos θ = 0
• Sur l'axes des x: mg sin θ = force qui tire l'objet vers le bas.

À l'équilibre, il faut exercer une force vers le haut pour maintenir l'objet stationnaire.

2. Équilibre sur un plan incliné
avec la force de laplace

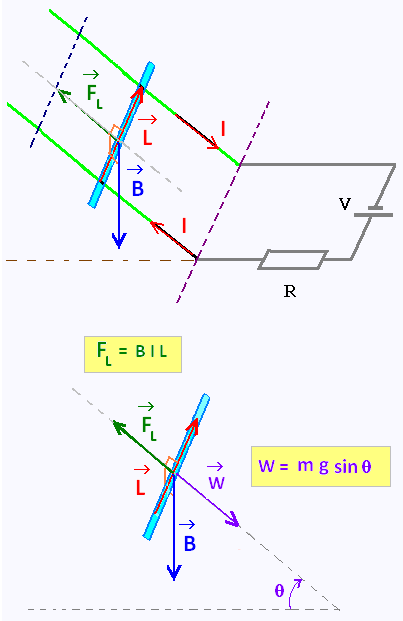
Cette force, c'est l'exemple la force de Laplace lorsque l'objet est ube barre metallique parcourue par un courant et plongée dans un champ magnétique.

Si le champ magnétique d'intensité B est dirigé vers le bas, et le courant électrique d'intensité I se dirige vers l'arrière, la force de laplace F, d'intensité BIL, formant un trièdre directe avec B et IL, point vers le haut du plan incliné et contrebalance ainsi le poids partiel m g sinθ.

À l'équlibre, on aura donc : m g sinθ = BIL

m g sinθ = BIL

Deux rails parallèles AD et A'D' distants de L = 12 cm sont inclinées à θ = 8^o avec l'horizontal.

Ces deux rails sont plongées dans un champ magnétique B dirigé vericalement vers le bas. Elles sont traversées par un courant d'intensité I = 2A.

Le circuit est fermé par une tige conductrice de longueur L et de masse m = 32 g, qui glisse sans frottement sur les rails.

La tige est immobile, donc, sur les rails de Laplace:

B = m g sinθ / IL

B = (0.032 x 10 x sin 8)/(2 x 0.12) = 0.18 T

B = 0.18 T

3. Cadre indéformable dans
un champ magnétique

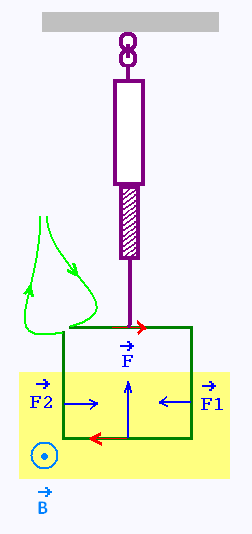
Un cadre rectangulaire indéformable , comportant N = 100 spires, est suspendu à un dynanomètre. Il est plongé partiellement dans un champ magétique uniforme B dirigé vers l'avant du plan et orthogonal au plan du cadre, qui est supposé vertical.

La longueur des brins horizontaux est égale à L = 15 cm. On suppose que les fils qui amènent le courant ne perturbent pas l'équilibre du cadre.

Lorsqu'un courant, d'intensité I = 0.5 A, est établi, le cadre devient soumis à 3 forces: F1 et F2 qui s'annulent mutuellement, puis F qui soulève le cadre et l'indication du dynamomètre augmente de F_o = 0.5 N. l'ensemble alors prend une position d'équilibre.

1) Les brins verticaux sont traversés par le courant dans deux sens opposés, quelque soit l'orientation du champ magnétique B ssur le cadre. Les forces qui y prennent alors place sont opposées et donc attractives et s'annulent mutuellement.

2) La force de Laplace a pour expression:

F = B I L N

On a donc: F = B I L N = F_o. D'où: B = F_o /I L N

B = F_o /I L N

B = 0.5/(0.5 x 0.15 x 100) = 1/15 = 0.067 = 66.7 mT

B = 66.7 mT

3) Si le champ magnétique B couvre le cadre au complet, alors, il n'y aura aucune force sur le dynamomètre, car les forces sur les deux brins horizontaux s'annuleront.

Remarque:

Il y a un champ magnétique induit par le cadre lorsqu'il est travesé par le courant électrique.

Si on assimile le cadre à un carré puis à un cercle de rayon R égal à la moitié de son arête L = 15 cm, alors le champ approximatif induit , au centre du cadre, est égal à:

B_induit = μ_oNI/2R =
4 π x 10^{- 7} x 100 x 0.5 / 2 x (0.15/2)
≈ 4 x 10^{- 4} T = 0.4 mT;
négligeable par rapport à B = 66.7 mT, utilisé .

4. Force de Laplace et cadres
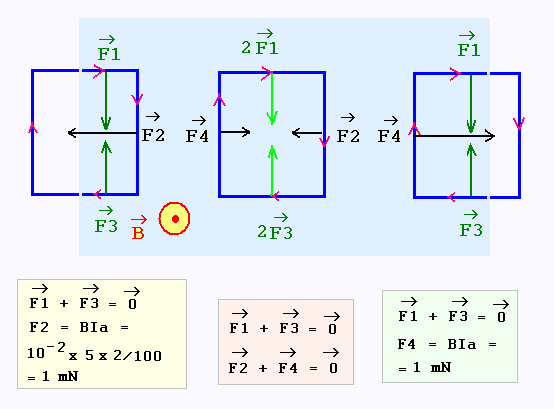