Physique 23 : Electricité et magnétisme
Force de Lorentz
Force de Laplace
1. Force électromagnétique de Lorentz
Une charge q qui se déplace avec une vitesse 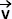 dans un champ électrique caractérisé par le
vecteur
dans un champ électrique caractérisé par le
vecteur 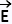 et dans un champ magnétique caractérisé par le
vecteur et dans un champ magnétique caractérisé par le
vecteur 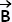 , subit une force magnétique appelée force de Lorentz , subit une force magnétique appelée force de Lorentz 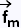 donnée par :
donnée par :
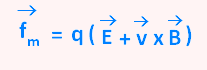
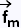 est le produit par la charge q
de la particule par la somme du champ
électrique est le produit par la charge q
de la particule par la somme du champ
électrique 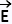 et du produit vectoriel de et du produit vectoriel de 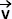 par par 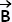 . .
2. Force magnétique de Lorentz
2.1. Définition
Une charge q qui se déplace avec une vitesse 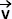 dans un champ magnétique caractérisé par le
vecteur
dans un champ magnétique caractérisé par le
vecteur 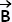 subit une force magnétique appelée force de Lorentz subit une force magnétique appelée force de Lorentz 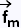 donnée par :
donnée par :
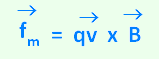
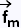 est le produit vectoriel de q est le produit vectoriel de q 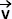 par par 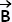 . .
2.2. Caractéristiques de la force de Lorentz
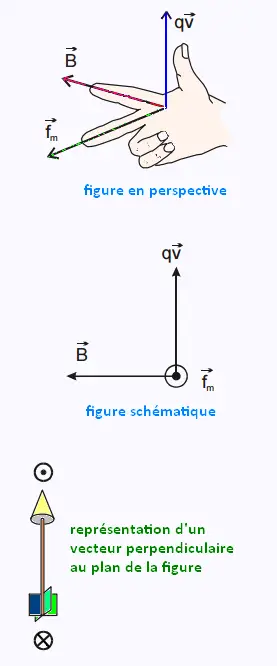
• direction : perpendiculaire à q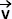 et à et à 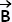 , donc au plan formé par q
, donc au plan formé par q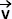 et et 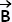
• sens : déterminé par la règle des trois doigts de la main droite :
pouce : sens de q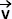 (= sens de
(= sens de 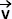 si q > 0 ou si q > 0 ou
= sens opposé à
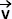 si q < 0) si q < 0)
index : sens de 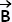
majeur : sens de 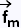
q est la charge de la particule en Coulomb(C)
v est la vitesse de la charge (m/s)
B est l'intensité (la norme) du vecteur champ magnétique en Tesla (T)
3. Force de Laplace
3.1. Définitions
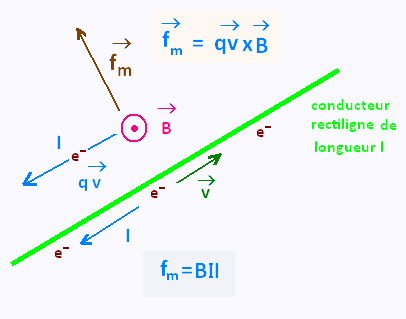
On considère un conducteur rectiligne de
longueur l parcouru par un courant
électrique d'intensité I et placé dans un
champ magnétique 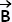 perpendiculaire au conducteur. Les N électrons libres contenus dans ce
conducteur et constituant le courant, de charge q = - e, se déplacent avec une
certaine vitesse
perpendiculaire au conducteur. Les N électrons libres contenus dans ce
conducteur et constituant le courant, de charge q = - e, se déplacent avec une
certaine vitesse 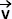 à travers
à travers 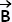 . .
Ils subissent donc tous une force de Lorentz :
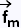 La résultante
La résultante 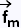 des N forces de Lorentz
constitue la force électromagnétique de
Laplace s'exerçant sur le conducteur tout
entier. des N forces de Lorentz
constitue la force électromagnétique de
Laplace s'exerçant sur le conducteur tout
entier.
Les N électrons libres se déplacent à la même
vitesse constante v. Dans ces conditions, les N électrons
subissent la même force de Lorentz 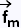 de module Fm = Nq v B sin (90o)
de module Fm = Nq v B sin (90o)
ΔQ = Nq est la charge totale traversant une section quelconque du
conducteur pendant la durée Δt.
Si Q = |Ne|, alors Δt = l/v durée qu'il faut aux N électrons présents dans le
conducteur pour s'écouler à travers une section. Donc:
Fm = Nq v B =
ΔQ v B = I Δt v B = I l B .
Force de Laplace : fm = = I l B .
3.2. Caractéristiques de la force de Laplace
Un conducteur de longueur l placé dans un champ magnétique 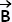 et parcouru par un courant I,
est soumis à une force de Laplace et parcouru par un courant I,
est soumis à une force de Laplace 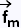 . .
• direction : perpendiculaire au plan formé par le conducteur et
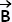
• sens : déterminé par la règle des trois doigts de la main droite
pouce : sens du courant
index : sens de 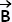
majeur : sens de 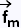 . .
• norme : fm = IBlsin(α)
où I est l'intensité de courant (A)
B est l'intensité (la norme) du vecteur champ magnétique (T)
α est l'angle formé par B par rapport au conducteur.
4. Vecteur champ électrique
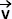 Une charge témoin > 0 est placée en un point M où
règne un champ électrique
Une charge témoin > 0 est placée en un point M où
règne un champ électrique 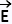 . Elle
subit une force électrique . Elle
subit une force électrique  qui dépend de la valeur de la charge q.
qui dépend de la valeur de la charge q.
Cette force s'exprime par :
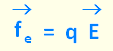
Cette formule F = q E découle de la loi de Coulomb:
fe = k qoq/r2 =
qo(k q /r2) = qo E
,
avec
E = k qo/r2
Le champ electrique 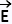 est crée par
la charge qo où on a placé la charge temoin q est crée par
la charge qo où on a placé la charge temoin q
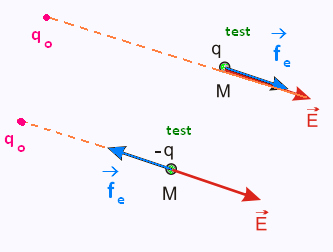
La force électrique  et le champ electrique et le champ electrique 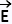 ont le même
sens si la charge témoin q est positive, de sens contraire si q est négative. ont le même
sens si la charge témoin q est positive, de sens contraire si q est négative.
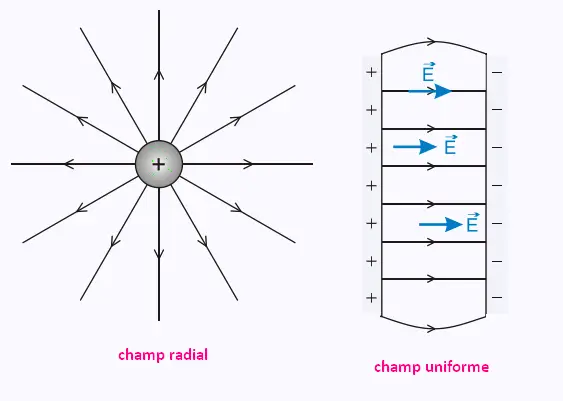
Voici deux types de ligne de champ: Un champ radial et un
champ uniforme:
5. Force électromagnétique de Laplace
sur un conducteur mobile dans un champ
magnétique
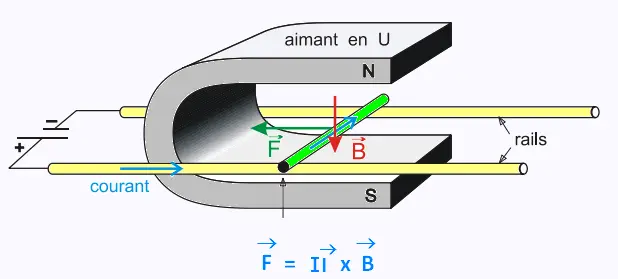
Voici un dispositif qui permet de mettre en évidence la force électromagnétique
de Laplace s'exerçant sur un conducteur parcouru par le courant et placé dans un champ magnétique
Un conducteur mobile est placé sur deux rails horizontaux connectés à un accumulateur, et
dans le champ magnétique d'un aimant en U.
Lorsque le courant passe, le conducteur mobile roule vers la gauche où vers la droite selon le
sens du courant et selon le sens du champ magnétique.
|