Calculus: Identities and Newton's binomial
1. Some identities:
(a + b)2 = a2 + 2ab + b2
(a - b)2 = a2 - 2ab + b2
(a + b)(a - b) = a2 - b2
x3 + y3 = (x + y) (x2 - xy + y2)
x3 - y3 = (x - y) (x2 + xy + y2)
2. Newton's binomial:
(x + y)n = Σ C(n, k) xn - k y k
k from 0 to ∞
C(n, k) = n!/k!(n - k)!
We have the following property:
C(n, k) = C(n - 1, k - 1) + C(n - 1, k)
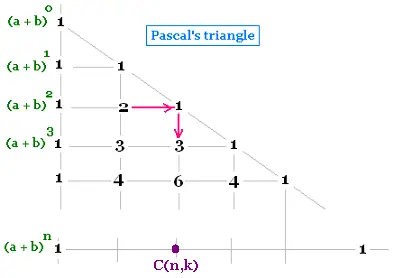
3. Particular case x = 1:
If x = 1, then
(1 + y)n = Σ C(n, k) yk
k from 0 to ∞
= 1 + n y + [ n(n - 1)/2!]y2 + [n(n - 1)(n - 2)/3!]y3 + ...
4. Exercises
Give the development of:
(a + b)5
(1 + 4)7
Solutions
|