Precalculus
Algebra
Trigonometry
Exponentials & Logarithms
Polynomials
Related exams
Related notes
© The scientific sentence. 2010
|
Precalculus: Exam 02 Solutions
Bien se rappeler des formules suivantes:
a)
A propos des in�quations et valeurs absolues:
Pour que �a soit complet, nous avons:
a > 0:
|f(x)| < a → - a < f(x) < a
|f(x)| > a → - a > f(x) et f(x) > a
a < 0 :
|f(x)| < a → Pas de solutions.
|f(x)| > a → Tout r�el est solution.
b)
Si sin x = a, alors x = arcsin (a) + 2kπ
Si cos x = a, alors x = arccos(a) + 2kπ
Si tan x = a, alors x = arctan(a) + kπ
(k est un nombre relatif).
c)
loga (ax) = x
ou
aloga(x) = x
loga a = 1
loga 1 = 0
a0 = 1 (a ≠1)
loga(x.y) = loga(x) + loga (y)
loga(x/y) = loga(x) - loga (y)
loga(xb) = b . loga(x)
Formule de changement de base:
loga x = logb x . loga b
d) Lorsque deux angles sont compl�mentaires (leur
somme est �gale � 90°), le sinus
de l'un est �gal au cosinus de l'autre et inversement.
e)
Toujours v�rifier le r�sultat en rempla�ant la valeure trouv�e
dans l'equation propos�e.
I) R�soudre les in�quations suivantes:
a)
3 x - 1 < 11
3 x - 1 < 11
3x < 1 + 11
3x < 12
x < 12/3
x < 4
S = ]- ∞ + 4[
b)
x(x - 1)( x + 4) > 0
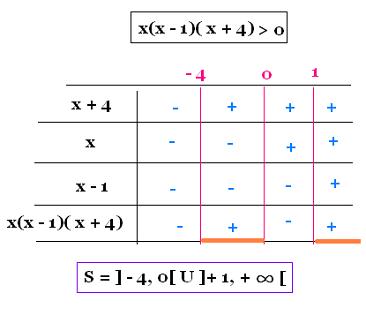
II) R�soudre les equations suivantes:
a) |2x - 4| = - 5
Impossible.
b) |2 x + 3| < 2
|2 x + 3| =
+(2 x + 3)
-(2 x + 3)
(2 x + 3) < 2 → x <(2 - 3)/2 → x < - 1/2
- (2 x + 3) < 2 → 2 x + 3 > - 2 → x > - 5/2
S = ]- 5/2, - 1/2[
c) |2 x + 3| > - 3
N'importe quel r�el est une solution.
S = R = S = ]-∞ + ∞[
III) R�soudre les equations suivantes:
a) x = sin (7π/3)
= sin (2π + π/3) = sin (π/3) = √3/2
b) cos (2x - 2 ) = √3/2
2x - 2 = Arccos (√3/2 ) = π/6 + 2k π
x = (π/6 + 2k π + 2)/2
c) sin x = cos x
On sait que:
cos2x + sin2x = 1.
Donc, compte tenu de sinx = cos, on a:
2 sin2x = 1.
Donc sin x = ± √2/2
Il vient:
x = arcsin (± √2/2) + 2kπ
x = ± π/4 + 2kπ
La valeur n�gative ne convient pas. Il
reste:
x = + π/4 + 2kπ
k est un entier relatif.
IV) Simplifier les expressions suivantes:
a) ln(a2 b3 c-7)
= 2 ln a + 3 ln b -7 ln c
b) log2(43 a2/b5/4)
=
3 log24 + 2log2 a - (5/4)log2 b
c) log[4 a3/(b2- 1)]
=
log 4 + 3 log a - log(b2 - 1)
V) R�soudre les equations suivantes:
a) ln (2 + 2 x) = 0
2 + 2 x = 1
x = -1/2
b) 3 + 4 ln(x - 3) = 1
4 ln(x - 3) = 1 - 3 = - 2
ln(x - 3) = - 2 /4 = - 2
eln(x - 3) = e-2
x - 3 = 1/e2
x = 1/e2 + 3
c) 3 + 4 log(x + 6) = - 1
4 log(x + 6) = - 1 - 3 = - 4
log(x + 6) = - 4/4 = -1
x + 6 = e-1 = 1/e
x = 1/e - 6
d) log1/2(3/x ) = 3
(1/2)log1/2(3/x) =
(1/2)3
3/x = (1/2)3
x = 3 /(1/2)3 = 3 /(1/8) = 24
VI) R�soudre les equations suivantes:
a) 10x+5 - 20 = 30
10x + 5 = 50
(x + 5) log 10 = log 30
(x + 5) . 1 = log 30
x + 5 = log (3 . 10) = log 3 + log 10
x + 5 = log 3 + 1
x = - 4 + log 3
b) 9 - 7 e2x = 2
- 7 e2x = 2 - 9 = - 7
e2x = 1
ln e2x = ln 1 = 0
2x = 0
x = 0
c) 102x = 2
2x = log 2
x = (1/2) log 2
d) e-3x = - 2
Impossible: An exponential is never
negative. It is always positive.
VII) Effectuer les divisions suivantes:
a) (x2 - 5 x + 6)/(x - 3) = x - 2 + 0 = x - 2
b) (x2 + 2 x + 4)/(x + 1) =
= (x + 1)2 + 3
VIII) D�composer en fractions partielles
les
fonctions rationnelles suivantes:
a) 16/(x - 3)(x + 5)
Pour cette fonction, donner les
valeurs des coefficients.
1/(x - 3)(x + 5) = a/(x - 3) + b/(x + 5)
=
a(x + 5)/(x - 3)(x + 5) + b(x - 3)/(x + 5)(x - 3) =
(a x + bx + 5 a - 3 b)/(x + 5)(x - 3) =
so
16/(x - 3)(x + 5) = (a x + bx + 5 a - 3 b)/(x + 5)(x - 3)
= ((a + b)x + 5 a - 3 b)/(x + 5)(x - 3)
Apr�s r�duction au m�me d�nominateur, on �galise les num�rateurs et puis
les termes correspondant � chacun des degr�s. On trouve:
a + b = 0
16 = 5 a - 3 b
so
b = - 2
a = 2
Then:
1/(x - 3)(x + 5) = 2/(x - 3) - 2/(x + 5)
b) (5x - 3)/(x - 2)(x + 5)2
= a/(x - 2) + b/(x + 5) + c/(x + 5)2
c) (x + 1)/x2 (x - 1)
= a/x + b/x2 + c/(x - 1)
Or
= ( a x + b)/x2 + c/(x - 1)
d) (2x - 1)/(x + 3)2(x2 + 1)3
= a/(x + 3) + b/(x + 3)2 +
(c x + d)/(x2 + 1) +
(e x + f)/(x2 + 1)2 +
(g x + h)/(x2 + 1)3 .
|
|
|