Precalculus: Solving inequalities
1. Worked example
We have the expression:
f(x) = x2 - x - 2, and
want to solve the following inequality:
f(x) <= 0
Two steps:
1. Factor the expression f(x)
x2 - x - 2 = (x + 1) (x - 2)
Then the roots of f(x) = 0 are
x = - 1, and
x = + 2
2. We draw the sign table as follows:
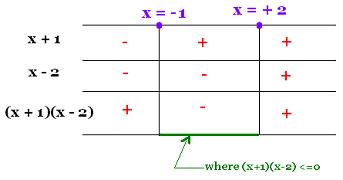
Therefore the solution of this inequality is
- 1 <= x <= 2, or the domain where f(x) is <= 0 is
D = [- 1, + 2].
2. Exercises
Solve each of the following inequalities:
x2 - 1 > 0
x2(x - 5) >=0
(x - 1)/ (x + 5) >= 0
x/( x - 1) <= 2
(x2 - 6 x + 8)/( x+ 2) < 0
Solutions
|