Precalculus: Notes 1
1.Be careful when using factoring by grouping
method and its particular case:
See these two examples:
factoring by grouping
f(x) = 2 x2 - 6x + 4 = 0
of the form :
a x2 + b x + c = 0
Somme x1 + x2 = - 6
Produit x1 . x2 = 2 . 4 = 8
Hence:
x1 = - 4
x2 = - 2
f(x) = (1/a)(ax + m)(ax + n)
2 x2 - 6x + 4 = (1/2)(2x - 4)(2x - 2) =
(x - 2)(2x - 2) = 2(x - 2)(x -1)
Always simplify the expressions.
Its particular case
f(x) = x2 - 9x + 14 = 0
of the form:
x2 - Sx + P = 0
Somme x1 + x2 = 9
Produit x1 . x2 = 14
x1 = 2
x2 = 7
f(x) = (x - x1)(x - x2)
f(x) = (x - 2)(x - 7)
2. sinus is an even function
sin2x + cos2x = 1 (1)
cos(x + y) = cosx cosy - sinx siny (2)
sin(x + y) = sinx cosy + cosx siny (3)
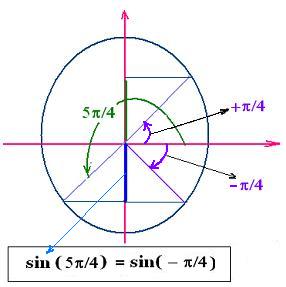
5π/4 = π + π/4
sin (5π/4) = sin (π + π/4)
Applying the relationship (3) yields:
sin(π + π/4) = sinπ cos(π/4) + cosπ sin(π/4)
we have
sinπ = 0
cosπ = - 1
Therefore
sin (5π/4) = 0. cos(π/4) -1 . sin(π/4) =
- sin(π/4)
Since sin is an even function
- sin(π/4) = sin(- π/4)
Therefore:
sin (5π/4) = sin(- π/4)
|