Precalculus: Trigonometric equations
1.Trigonometric equations
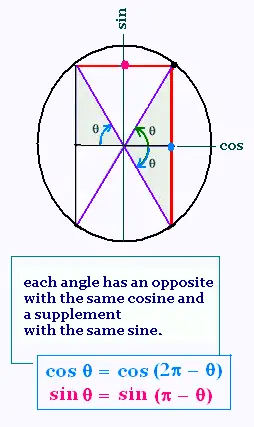
Here are the rules:
sin (x ) = a
x = arcsin (a) + 2kπ
x = π - arcsin (a) + 2kπ
cos(x) = a
x = arccos (a) + 2kπ
x = 2π - arccos (a) + 2kπ
tan(x) = a
x = arctan(a) + kπ
k is an integer.
2. Worked examples
1.
sin (x ) = 1/2
x = π/6 + 2kπ
x = π - π/6 + 2kπ = 5π/6 + 2kπ
2.
cos(x ) = 1/2
x = π/3 + 2kπ
x = 2π - π/3 + 2kπ = 5π/3 + 2kπ
3.
cos(x) = sin (x)
tan (x) = 1
x = arctan(1) + kπ
x = π/4 + kπ
4.
sin 2x = sin x for x ∊ [0, 2π[ .
sin 2x = sin x
2 sin x cos x = sin x
2 sin x cos x - sinx = 0
(sin x)(2 cos x - 1) = 0
sin x = 0 or cos x = 1
sin x = 0
First solution:
sin 0 = 0 , then
x = 0
x = π - 0 = π
cos x = 1/2
First solution:
x = π/3, then
x = π/3
x = 2π - π/3 = 5π/3
Within the interval [0, 2π[, the solutions
are
{0,π/3,5π/3,π }
5.
2 sin2 x + sin x - 1 = 0
(2 sin x - 1)(sin x + 1) = 0
sin x = 1/2 or sin x = - 1
sin x = 1/2:
sin x = 1/2 = sin π/6 (first solution), then
x = π/6
x = π - π/6 = 5π/6
sin x = - 1:
sin x = - 1 = sin (3π/2) (one solution), then
x = 3π/2
Within the interval [0, 2π[, the solutions
are
{π/6, 3π/2, 5π/6}
3. Related figures
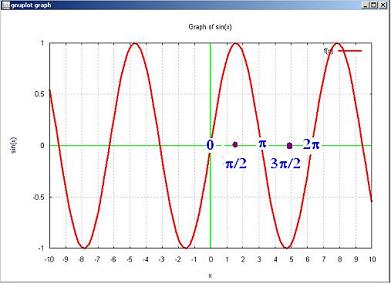
1. Graph of sin(x)
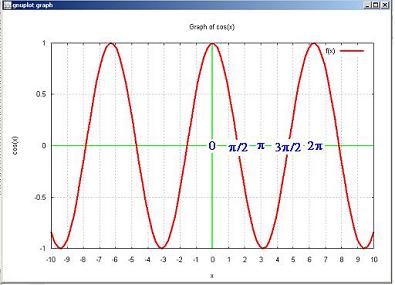
2. Graph of cos(x)
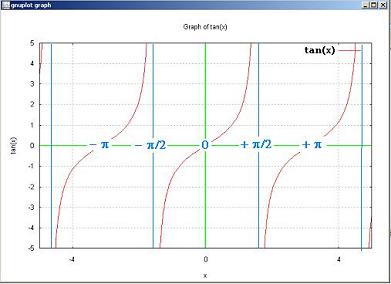
3. Graph of tan(x)
4. Properties
The functions sin(x) and cos(x) are
periodic.
The period is 2π.
cos (x ) = cos (x + 2πk)
sin(x ) = sin (x + 2πk)
k is an ineger.
The function tan(x) is
periodic.
The period is π.
tan (x) = tan (x + πk)
k is an ineger.
The function cos(x) is even. That is:
cos (x) = cos (- x)
The function sin (x) is odd. That is:
sin(- x) = - sin (x)
The function tan(x) is odd. That is:
tan(- x) = - tan(x)
5. Exercises
1. Solve for x each of the following:
2 cos (x - 2) = 1
sin (2x - 5 ) = - √2 /2
sin (3x) = 3
tan (x - 2) = - 1
2. Find graphically the intersection points
of the two functions sin(x) and cos(x)
Solutions
|